The sun is a spherical source of about 1.39 million km diameter, at an average distance (1 astronomical unit) of 149.6 million km from earth. The direct portion of the solar radiation is collimated with an angle of approximately 0.53° (full angle), while the “diffuse” portion is incident from the hemispheric sky and from ground reflections and scatter. The “global” irradiation, the sum of the direct and diffuse components, is essentially uniform. Since there is a strong forward distribution in aerosol scattering, high aerosol loading of the atmosphere leads to considerable scattered radiation appearing to come from a small annulus around the solar disk, the solar aureole. This radiation mixed with the direct beam is called circumsolar radiation.
The solar disk subtends a 1/2° angle at the earth.
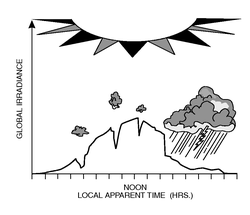
Dirunal and Annual Variation – Below figures show typical diurnal variations of global solar radiative flux. Actual halfwidth and peak position of the curve shape depend on latitude and time of year. Fig. 1 shows a cloudless atmosphere. Fig. 2 shows the impact of clouds. Fig. 2 shows the global solar irradiance at solar noon measured in Arizona, showing the annual variation.
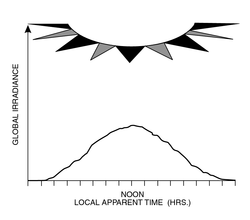
Fig. 1 Diurnal variations of global solar radiative flux on a sunny day.

Fig. 2 Diurnal variations of global solar radiative flux on a cloudy day.
The global solar irradiance at solar noon measured in Arizona, showing the annual variation.
Solar Geometry
When designing any type of system that relies on solar radiation, it is important to take into consideration the seasonal and hourly changes in position of the sun. This has a direct influence on the incident angle of sunlight, so it is valuable to incorporate a system that can adjust to the position of the sun. It is also helpful to consider the position of the sun when deciding the placement of a structure’s windows.

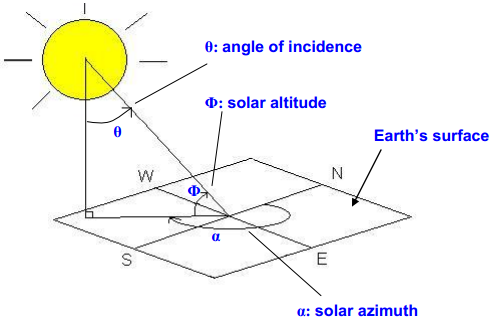
The position of the sun can be described by two different angles. The first angle is the solar azimuth (denoted by α, alpha), which is defined as the clockwise angle between the sun and the cardinal direction of true north. It is measured up to the horizontal projection of the sun’s position onto the Earth’s surface (see Figure below). The second angle is the solar altitude or elevation (denoted by Φ, phi), indicating the angle of the sun’s position from the horizontal (see Figure below). The angle of incidence is not a measure of the sun’s position, but rather a measure of the amount of radiation incident on a vertical surface. The angle of incidence is related to the solar altitude as
Together, the two angles provide useful information about the orientation of incoming sunlight on an object or structure. Knowing this, solar collectors and other devices should be installed so they are within 20° of either side of perpendicular to the sun. By incorporating a system that adjusts to the incident angle of the sun, we can further control the angle incident on the surface of the collector. For example, hinging light shelves so they are adjustable for the optimal angle.
Tilt of the Earth
The Earth is tilted about 23.5°on its pole-to-pole axis, relative to the horizontal plane of its orbit. This results in a 47° peak solar altitude angle difference, causing the hemisphere-specific difference between summer and winter. In the northern hemisphere, the sun remains on the south-facing (equator-facing) side of the house all day long, and varies in its incident angle.
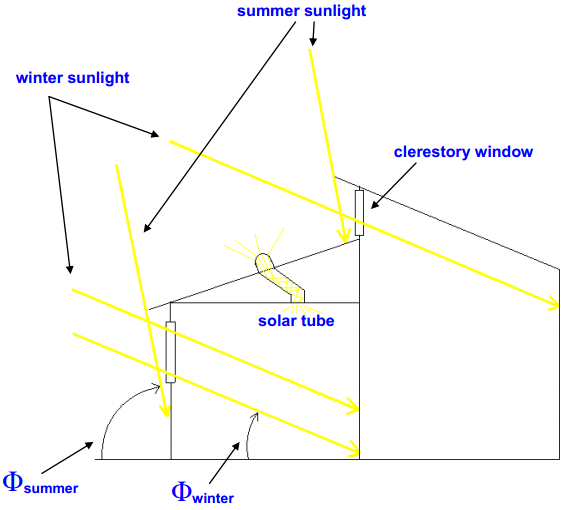
In the northern hemisphere, due to the Earth’s tilt, the solar altitude approaches its minimum during the winter; the converse is true during the summer. This is critical to take into consideration when designing a structure’s windows and shading (see Figure below). Because of the reduced solar altitude during the cold season, desirable radiation and natural light can enter deep into the interior space. While the strategic placement of roof overhangs above the windows prevents undesirable extra sunlight radiation from entering a space during the hot season.
Estimating The Availability Of Solar Raditaions
In practical studies it is logical to consider that the solar radiation is directly proportional to the sunshine duration. The formulation of the proportionality can be derived from the measurements of the variables through scatter diagrams and most often by the application of statistical regression methods. The original models in solar energy expressed this relationship between solar radiation and the sunshine duration as linear. Such a pioneering relationship was presented by Angström in 1924.
Angstrom Model – The original Angstrom-type regression equation related monthly average daily radiation to clear day radiation in a given location and average fraction of possible sunshine hours
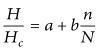
where H = monthly average daily global radiation (Wh/m2/day), Hc = monthly average clear sky daily global radiation for the location in a given day, n = actual sunshine duration in a day, respectively, (hours), average maximum possible bright sunshine duration in a day and also known as monthly mean length of the day in hours, a and b = empirical coefficients. These coefficients are location-specific coefficients referred to as fractions of extraterrestrial radiation on overcast days and on average days, respectively.
The ratio n/N is referred to as cloudless index. It gives information about atmospheric characteristics and conditions of the study area.
Angstrom-Prescott Model – A basic difficulty with above model lies in the definition of the terms n/N and Hc. Because there may be problems in calculating clear sky radiation accurately, this model was modified by Prescott in 1940 by replacing clear sky radiation with extraterrestrial radiation Ho. This model popularly known as the Angstrom-Prescott model is the most commonly used model and is given by
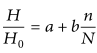
where Ho is the monthly average daily extraterrestrial radiation.
The ratio of solar radiation at the surface of the Earth (H) to extraterrestrial radiation (Ho), that is, H/Ho, is called the Clearness Index. Values of the monthly average daily extraterrestrial radiation (Ho) is calculated from the following
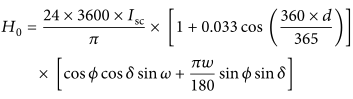
where Isc = solar constant with a value of 1367Wm-2, d = day of the year from January 1 to December 31 taking January 1st as 1, = latitude of the location, = declination angle, = sunset hour angle and .

