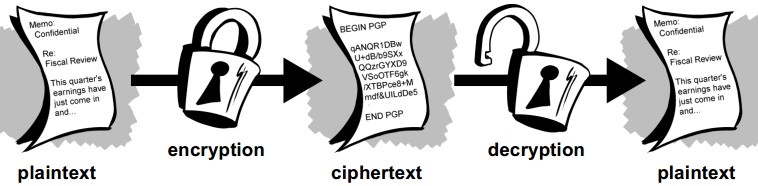
Data that can be read and understood without any special measures is called plaintext or cleartext. The method of disguising plaintext in such a way as to hide its substance is called encryption. Encrypting plaintext results in unreadable gibberish called ciphertext. You use encryption to ensure that information is hidden from anyone for whom it is not intended, even those who can see the encrypted data. The process of reverting ciphertext to its original plaintext is called decryption.
Essential Elements
There are three critical elements to data security. Confidentiality, integrity, and authentication are known as the CIA triad Data encryption provides confidentiality, message hashing provides integrity and message digital signatures provide authentication. Cryptography offers the following four basic elements
- Confidentiality – It is assurance that only authorized users can read or use confidential information.
- Authentication – It is the verification of the identity of the entities that communicate over the network.
- Integrity – It is the verification that the original contents of information have not been altered or corrupted.
- Non-repudiation – It is the assurance that a party in a communication cannot falsely deny that a part of the actual communication occurred.
Important Cryptography Terms
- Algorithm – Set of mathematical rules used in encryption and decryption.
- Cryptography – Science of secret writing that enables you to store and transmit data in a form that is available only to the intended individuals.
- Cryptosystem – Hardware or software implementation of cryptography that transforms a message to ciphertext and back to plaintext.
- Cryptanalysis – Practice of obtaining plaintext from ciphertext without a key or breaking the encryption.
- Ciphertext – Data in encrypted or unreadable format.
- Encipher – Act of transforming data into an unreadable format.
- Decipher – Act of transforming data into a readable format.
- Key – Secret sequence of bits and instructions that governs the act of encryption and decryption.
- Key clustering – Instance when two different keys generate the same ciphertext from the same plaintext.
- Keyspace – Possible values used to construct keys Plaintext Data in readable format, also referred to as cleartext.
Cryptographic Algorithms Types
There are several ways of classifying cryptographic algorithms like categorization based on the number of keys that are employed for encryption and decryption, defined by their application and use. The three types of algorithms that are usually classified into are
- Secret Key Cryptography (SKC) – Uses a single key for both encryption and decryption
- Public Key Cryptography (PKC) – Uses one key for encryption and another for decryption
- Hash Functions – Uses a mathematical transformation to irreversibly “encrypt” information
Symmetric and Asymmetric key Cryptography
The two primary types of encryption are symmetric and asymmetric key encryption.
Symmetric Key Encryption – It means both sender and receiver use the same secret key to encrypt and decrypt the data. A secret key, which can be a number, a word, or just a string of random letters, is applied to the text of a message to change the content in a particular way. This might be as simple as shifting each letter by a number of places in the alphabet.
As long as both sender and recipient know the secret key, they can encrypt and decrypt all messages that use this key. The drawback to symmetric key encryption is there is no secure way to share the key between multiple systems. Systems that use symmetric key encryption need to use an offline method to transfer the keys from one system to another. This is not practical in a large environment such as the Internet, where the clients and servers are not located in the same physical place. The strength of symmetric key encryption is fast, bulk encryption. Weaknesses of symmetric key encryption are key distribution, scalability, limited security (confidentiality only) and The fact that it does not provide non-repudiation, meaning the sender’s identity can be proven.
Examples of symmetric algorithms are DES (data encryption standard), 3DES, AES (Advanced Encryption Standard), IDEA (International Data Encryption Algorithm), Twofish, RC4 (Rivest Cipher 4)
Asymmetric (or public) key cryptography – It was created to address the weaknesses of symmetric key management and distribution. But there’s a problem with secret keys: how can they be exchanged securely over an inherently insecure network such as the Internet?
Anyone who knows the secret key can decrypt the message, so it is important to keep the secret key secure. Asymmetric encryption uses two related keys known as a key pair. A public key is made available to anyone who might want to send you an encrypted message. A second, private key is kept secret, so that only you know it. Any messages (text, binary files, or documents) that are encrypted by using the public key can only be decrypted by using the matching private key. Any message that is encrypted by using the private key can only be decrypted by using the matching public key. This means that you do not have to worry about passing public keys over the Internet as they are by nature available to anyone. A problem with asymmetric encryption, however, is that it is slower than symmetric encryption. It requires far more processing power to both encrypt and decrypt the content of the message.
The relationship between the two keys in asymmetric key encryption is based on complex mathematical formulas. One method of creating the key pair is to use factorization of prime numbers. Another is to use discrete logarithms. Asymmetric encryption systems are based on one-way functions that act as a trapdoor. Essentially the encryption is one-way in that the same key cannot decrypt messages it encrypted. The associated private key provides information to make decryption feasible. The information about the function is included in the public key, whereas information about the trapdoor is in the private key.
Anyone who has the private key knows the trapdoor function and can compute the public key. To use asymmetric encryption, there needs to be a method for transferring public keys. The typical technique is to use X.509 digital certificates (also known simply as certificates). A certificate is a file of information that identifies a user or a server, and contains the organization name, the organization that issued the certificate, and the user’s email address, country, and public key.
When a server and a client require a secure encrypted communication, they send a query over the network to the other party, which sends back a copy of the certificate. The other party’s public key can be extracted from the certificate. A certificate can also be used to uniquely identify the holder. Asymmetric encryption can be used for Data encryption and Digital signatures.
Asymmetric encryption can provide Confidentiality, Authentication and Non-repudiation. Strengths of asymmetric key encryption include Key distribution, Scalability and confidentiality, authentication, and non-repudiation. The weakness of asymmetric key encryption is that the process is slow and typically requires a significantly longer key. It’s only suitable for small amounts of data due to its slow operation.
Private and Public Key Exchange
Key exchange also called as key establishment, is method to exchange cryptographic keys between users, using a cryptographic algorithm. If the cipher is a symmetric key cipher, both will need a copy of the same key. If an asymmetric key cipher with the public/private key property, both will need the other’s public key.
Prior to any secured communication, users must set up the details of the cryptography. In some instances this may require exchanging identical keys (in the case of a symmetric key system). In others it may require possessing the other party’s public key. While public keys can be openly exchanged (their corresponding private key is kept secret), symmetric keys must be exchanged over a secure communication channel.
Formerly, exchange of such a key was extremely troublesome, and was greatly eased by access to secure channels such as a diplomatic bag. Clear text exchange of symmetric keys would enable any interceptor to immediately learn the key, and any encrypted data.
The advance of public key cryptography in the 1970s has made the exchange of keys less troublesome. Since the Diffie-Hellman key exchange protocol was published in 1975, it has become possible to exchange a key over an insecure communications channel, which has substantially reduced the risk of key disclosure during distribution. It is possible, using something akin to a book code, to include key indicators as clear text attached to an encrypted message. The encryption technique used by Richard Sorge’s code clerk was of this type, referring to a page in a statistical manual, though it was in fact a code. The German Army Enigma symmetric encryption key was a mixed type early in its use; the key was a combination of secretly distributed key schedules and a user chosen session key component for each message.
In more modern systems, such as OpenPGP compatible systems, a session key for a symmetric key algorithm is distributed encrypted by an asymmetric key algorithm. This approach avoids even the necessity for using a key exchange protocol like Diffie-Hellman key exchange.
Another method of key exchange involves encapsulating one key within another. Typically a master key is generated and exchanged using some secure method. This method is usually cumbersome or expensive (breaking a master key into multiple parts and sending each with a trusted courier for example) and not suitable for use on a larger scale. Once the master key has been securely exchanged, it can then be used to securely exchange subsequent keys with ease. This technique is usually termed Key Wrap. A common technique uses Block ciphers and cryptographic hash functions.
A related method is to exchange a master key (sometimes termed a root key) and derive subsidiary keys as needed from that key and some other data (often referred to as diversification data). The most common use for this method is probably in SmartCard based cryptosystems, such as those found in banking cards. The bank or credit network embeds their secret key into the card’s secure key storage during card production at a secured production facility. Then at the Point of sale the card and card reader are both able to derive a common set of session keys based on the shared secret key and card-specific data (such as the card serial number). This method can also be used when keys must be related to each other (i.e., departmental keys are tied to divisional keys, and individual keys tied to departmental keys). However, tying keys to each other in this way increases the damage which may result from a security breach as attackers will learn something about more than one key. This reduces entropy, with regard to an attacker, for each key involved.
Two of the most common key exchange algorithms are
- Diffie-Hellman Key Agreement algorithm
- RSA key exchange process
Both methods provide for highly secure key exchange between communicating parties. An intruder who intercepts network communications cannot easily guess or decode the secret key that is required to decrypt communications. The exact mechanisms and algorithms that are used for key exchange varies for each security technology. In general, the Diffie-Hellman Key Agreement algorithm provides better performance than the RSA key exchange algorithm.
Diffie-Hellman Key Agreement – Public key cryptography was first publicly proposed in 1975 by Stanford University researchers Whitfield Diffie and Martin Hellman to provide a secure solution for confidentially exchanging information online. Figure 14.5 shows the basic Diffie-Hellman Key Agreement process.
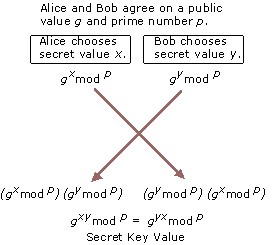
Diffie-Hellman key agreement is not based on encryption and decryption, but instead relies on mathematical functions that enable two parties to generate a shared secret key for exchanging information confidentially online. Essentially, each party agrees on a public value g and a large prime number p. Next, one party chooses a secret value x and the other party chooses a secret value y. Both parties use their secret values to derive public values, g x mod p and g y mod p, and they exchange the public values. Each party then uses the other party’s public value to calculate the shared secret key that is used by both parties for confidential communications. A third party cannot derive the shared secret key because they do not know either of the secret values, x or y.
For example, Alice chooses secret value x and sends the public value g x mod p to Bob. Bob chooses secret value y and sends the public value g y mod p to Alice. Alice uses the value g xy mod p as her secret key for confidential communications with Bob. Bob uses the value g yx mod p as his secret key. Because g xy mod p equals g yx mod p , Alice and Bob can use their secret keys with a symmetric key algorithm to conduct confidential online communications. The use of the modulo function ensures that both parties can calculate the same secret key value, but an eavesdropper cannot. An eavesdropper can intercept the values of g and p , but because of the extremely difficult mathematical problem created by the use of a large prime number in mod p, the eavesdropper cannot feasibly calculate either secret value x or secret value y . The secret key is known only to each party and is never visible on the network.
Diffie-Hellman key exchange is widely used with varying technical details by Internet security technologies, such as IPSec and TLS, to provide secret key exchange for confidential online communications. For technical discussions about Diffie-Hellman key agreement and how it is implemented in security technologies, see the cryptography literature that is referenced under
RSA Key Exchange – The Rivest-Shamir-Adleman (RSA) algorithms available from RSA Data Security, Inc., are the most widely used public key cryptography algorithms. For RSA key exchange, secret keys are exchanged securely online by encrypting the secret key with the intended recipient’s public key. Only the intended recipient can decrypt the secret key because it requires the use of the recipient’s private key. Therefore, a third party who intercepts the encrypted, shared secret key cannot decrypt and use it. The below figure illustrates the basic RSA key exchange process.
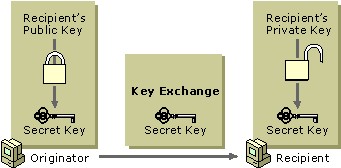
The RSA key exchange process is used by some security technologies to protect encryption keys. For example, EFS uses the RSA key exchange process to protect the bulk encryption keys that are used to encrypt and decrypt files.
Stream and Block Ciphers
Block ciphers and stream ciphers are the two types of encryption ciphers.
Block Ciphers – They are encryption ciphers that operate by encrypting a fixed amount, or “block,” of data. The most common block size is 64 bits of data. This chunk or block of data is encrypted as one unit of cleartext. When a block cipher is used for encryption and decryption, the message is divided into blocks of bits. Blocks are then put through one or more of the following scrambling methods like substitution, transposition, confusion and diffusion.
Stream Cipher – It encrypts single bits of data as a continuous stream of data bits. Stream ciphers typically execute at a higher speed than block ciphers and are suited for hardware usage. The stream cipher then combines a plain text bit with a pseudorandom cipher bit stream by means of an XOR (exclusive OR) operation.
Secret Key Cryptography
It is an encryption system in which the sender and receiver of a message share a single, common key that is used to encrypt and decrypt the message. Secret-key systems are simpler and faster, but their main drawback is that the two parties must somehow exchange the key in a secure way. Public-key encryption avoids this problem because the public key can be distributed in a non-secure way, and the private key is never transmitted. secret-key cryptography is also called symmetric-key cryptography. The most popular symmetric-key system is the Data Encryption Standard (DES).
DES – The Data Encryption Standard (DES) is a block cipher that uses shared secret encryption. It was selected by the National Bureau of Standards as an official Federal Information Processing Standard (FIPS) for the United States in 1976 and which has subsequently enjoyed widespread use internationally. It is based on a symmetric-key algorithm that uses a 56-bit key. The algorithm was initially controversial with classified design elements, a relatively short key length, and suspicions about a National Security Agency (NSA) backdoor. DES consequently came under intense academic scrutiny which motivated the modern understanding of block ciphers and their cryptanalysis.
DES is now considered to be insecure for many applications. This is chiefly due to the 56-bit key size being too small; in January, 1999, distributed.net and the Electronic Frontier Foundation collaborated to publicly break a DES key in 22 hours and 15 minutes. There are also some analytical results which demonstrate theoretical weaknesses in the cipher, although they are infeasible to mount in practice. The algorithm is believed to be practically secure in the form of Triple DES, although there are theoretical attacks. In recent years, the cipher has been superseded by the Advanced Encryption Standard (AES). Furthermore, DES has been withdrawn as a standard by the National Institute of Standards and Technology (formerly the National Bureau of Standards).
Triple DES – It is also referred to as 3DES, a mode of the DES encryption algorithm that encrypts data three times. Three 64-bit keys are used, instead of one, for an overall key length of 192 bits (the first encryption is encrypted with second key, and the resulting cipher text is again encrypted with a third key).
The National Institute of Standards and Technology (NIST) ratified the Advanced Encryption Standard (AES) as a replacement for DES. NIST endorsed Triple DES as an interim standard to be used until AES was finished. Although AES is at least as strong as Triple DES, it is significantly faster. Many security systems support both Triple DES and AES. AES is the default algorithm, while Triple DES is often maintained for backward compatibility.
Message Authentication
Message authentication allows one party—the sender—to send a message to another party—the receiver—in such a way that if the message is modified en route, then the receiver will almost certainly detect this. Message authentication is also called data-origin authentication. Message authentication is said to protect the integrity of a message, ensuring that each message that it is received and deemed acceptable is arriving in the same condition that it was sent out—with no bits inserted, missing, or modified.
Message authentication provides two services. It provides a way to ensure message integrity and a way to verify who sent the message. To request authentication, the sending application must set the authentication level of the message to be authenticated. Authenticating for message integrity ensures that no one has tampered with the message or changed its content.
There are two methods for producing the message authentication code:
- Data encryption standard (DES)
- Cyclic Redundancy Check (CRC)
Message Authentication Code – It is also called as MAC. A message authentication code (MAC) is a cryptographic checksum on data that uses a session key to detect both accidental and intentional modifications of the data. It is a security code that is typed in by the user of a computer to access accounts or portals. This code is attached to the message or request sent by the user. Message authentication codes (MACs) attached to the message must be recognized by the receiving system in order to grant the user access. MACs are commonly used in electronic funds transfers (EFTs) to maintain information integrity.
The message authentication code technique involves the use of a secret key to generate a small block of data that is appended to the message. This technique assumes that two communicating parties, say A and B, share a common secret key KAB. When A has a message to send to B, it calculates the message authentication code as a function of the message and the key: MACM = F (KAB,M). The message plus code are transmitted to the intended recipient. The recipient performs the same calculation on the received message, using the same secret key, to generate a new message authentication code. The received code is compared to the calculated code. If we assume that only the receiver and the sender know the identity of the key, and if the received code matches the calculate code, then
- The receiver is assured that the message has not been altered.
- The receiver is assured that the message is from the alleged sender. Because no one else knows the secret key, no one else could prepare a message with a proper code.
- If the message includes a sequence number, then the receiver can be assured of the proper sequence, because an attacker cannot successfully alter the sequence number.
A number of algorithms could be used to generate the code. The national Bureau of Standards, in its publication DES Modes of Operation, recommends the use of Data Encryption Algorithm (DEA).
Hash Functions
A hash function takes a group of characters (called a key) and maps it to a value of a certain length (called a hash value or hash). The hash value is representative of the original string of characters, but is normally smaller than the original. Hashing is used in encryption and also done for indexing and locating items in databases.
A hash function maps keys to small integers (buckets). An ideal hash function maps the keys to the integers in a random-like manner, so that bucket values are evenly distributed even if there are regularities in the input data. This process can be divided into two steps as
- Map the key to an integer.
- Map the integer to a bucket.
Simple hash functions map a single integer key (k) to a small integer bucket value h(k). m is the size of the hash table (number of buckets). Few simple hash function are
- Division method (Cormen) Choose a prime that isn’t close to a power of 2. h(k) = k mod m. Works badly for many types of patterns in the input data.
- Knuth Variant on Division h(k) = k(k+3) mod m. Supposedly works much better than the raw division method.
Hash functions chop up the input data and make mess of it so that the original data would be difficult or impossible to deduce from the mangled remains. Value provides a way of checking whether the message has been manipulated or corrupted in transit or storage. It is a sort of “digital fingerprint”. Moreover, the message digest can be encrypted using either conventional or public-key cryptography to produce a digital signature, which is used to help the recipient feel confident that the received message is not forget. The hash function H must satisfy following conditions
- It should be one-way: For a given hash value v =H(x) it should be infeasible for an opponent to find a message x such that x= H-1(v).
- It should at least be weakly collision resistant: Given a hash value v =H(x) and the message x from which it was computed, it should be computationally infeasible for an opponent to find another message y different from x such that v =H(y).
It might be strongly collision resistant: It is computationally infeasible for an opponent to find a pair of distinct messages x and y such that H(x)=H(y).

