Design of Experiments (DOE)

Let us discuss the Design of Experiments DOE. 

It is a method of varying a number of input factors simultaneously in a planned manner, so that their individual and combined effects on the output can be identified. It develops well-designed efforts to identify which process changes yield the best possible results for sustained improvement as mostly experiments address only one factor at a time, the Design of Experiments (DOE) method focuses on multiple factors at one time. It provides the data that illustrates the significance to the output of input variables acting alone or interacting with one another.

Basic terms

Basic DOE terms are –

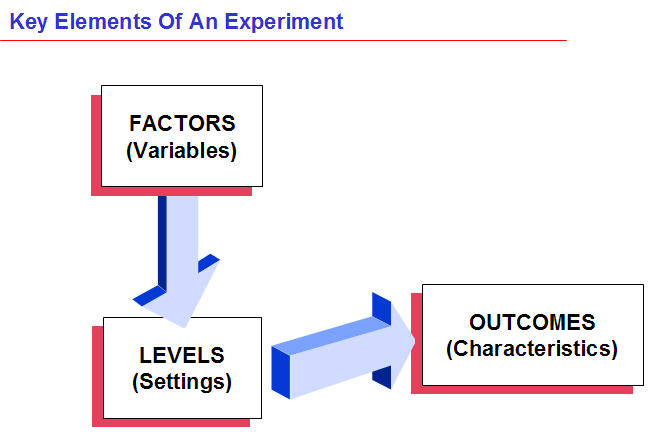
• Factor – A predictor variable that is varied with the intent of assessing its effect on a response variable. Most often referred to as an “input variable.”
• Factor Level – It is a specific setting for a factor. In DOE, levels are frequently set as high and low for each factor. A potential setting, value or assignment of a factor of the value of the predictor variable like, if the factor is time, then the low level may be 10 minutes and the high level may be 30 minutes.
• Response variable – A variable representing the outcome of an experiment. The response is often referred to as the output or dependent variable.
• Treatment – The specific setting of factor levels for an experimental unit. For example, a level of temperature at 65° C and a level of time at 45 minutes describe a treatment as it relates to an output of yield.
• Experimental error – An error from an experiment reveals variation in the outcome of identical tests. The variation in the response variable beyond that accounted for by the factors, blocks, or other assignable sources while conducting an experiment.
• Experimental run – A single performance of an experiment for a specific set of treatment conditions.
• Experimental unit – The smallest entity receiving a particular treatment, subsequently yielding a value of the response variable.
• Predictor Variable – A variable that can contribute to the explanation of the outcome of an experiment. Also known as an independent variable.
• Repeated Measures – The measurement of a response variable more than once under similar conditions. Repeated measures allow one to determine the inherent variability in the measurement system. Repeated measures are known as “duplication” or ‘repetition.”
• Replicate – A single repetition of the experiment.
• Replication – Performance of an experiment more than once for a given set of predictor variables. Each of the repetitions of the experiment is called a “replicate.” Replication differs from repeated measures in that it is a repeat of the entire experiment for a given set of predictor variables, not just repeat of measurements of the same experiment. Replication increases the precision of the estimates of the effects in an experiment. Replication is more effective when all elements contributing to the experimental error are included. In some cases replication may be limited to repeated measures under essentially the same conditions. In other cases, replication may be deliberately different, though similar, in order to make the results more general.
• Repetition – When an experiment is conducted more than once, repetition describes this event when the factors are not reset. Subsequent test trials are run again but not necessarily under the same conditions.
• Blocking – When structuring fractional factorial experimental test trials, blocking is used to account for variables that the experimenter wishes to avoid. A block may be a dummy factor which doesn’t interact with the real factors.
• Box-Behnken – When full second-order polynomial models are to be used in response surface studies of three or more factors, Box- Behnken designs are often very efficient. They are highly fractional, three-level factorial designs.
• EVOP – It stands for evolutionary operation, a term that describes the way sequential experimental designs can be made to adapt to system behavior by learning from present results and predicting future treatments for better response.
• First-order – It refers to the power to which a factor appears in a model. If “X1” represents a factor and “B” is its factor effect, then the model Y = B0 + B1X1 + B2X2 + ,is first-order in both X1 and X2.
• Fractional – An adjective that means fewer experiments than the full design.
• Full Factorial – It describes experimental designs which contain all combinations of all levels of all factors. No possible treatment combinations are omitted.
• Paired Comparison – The basis of a technique for treating data so as to ignore sample-to-sample variability and focus more clearly on variability caused by a specific factor effect. Only differences in response for each sample are tested because sample-to-sample differences are irrelevant.
• Fixed Effects Model – If the treatment levels are specifically chosen by the experimenter, then conclusions reached will only apply to those levels.
• Random Effects Model – If the treatment levels are randomly chosen from a population of many possible treatment levels, then conclusions reached can be extended to all treatment levels in the population.
• Residual Error () or (E) – The difference between the observed and the predicted value for that result, based on an empirically determined model. It can be variation in outcomes of virtually identical test conditions.
• Residuals – The difference between experimental responses and predicted model values.
• Resolution – A fractional factorial design in which no main effects are confounded with each other but the main effects and two factor interaction effects are confounded.

ANOVA is a basic step in the DOE that is a formidable tool for decision-making based on data analysis. The types of ANOVA that are more commonly used are:

• The completely randomized experimental design, or one-way ANOVA. One-way ANOVA compares several (usually more than two) samples’ means to determine if there is a significant difference between them.
• The factorial design, or two-way ANOVA, which takes into account the effect of noise factors.

 Randomized Block Plans
When each homogeneous group in the experiment contains exactly one measurement on every treatment, the experimental plan is called a randomized block plan. For example, an experimental scheme may take several days to complete.

Latin Square Designs
A Latin square plan is useful to allow for two sources of non-homogeneity in the conditions affecting test results. A third variable, the experimental treatment, is then applied to the source variables in a balanced fashion.

Full and Fractional Factorial
A full factorial is an experimental design which contains all levels of all factors. No possible treatments are omitted. A fractional factorial is a balanced experimental design which contains fewer than all combinations of all levels of all factors.

Taguchi Designs
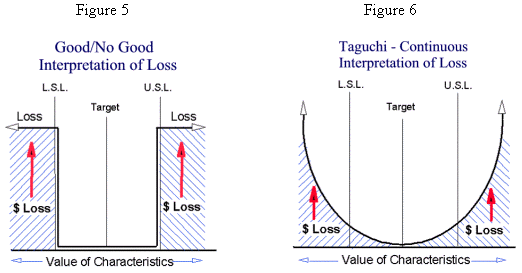
The Taguchi philosophy emphasizes two tenets of reducing the variation of a product or process which reduces the loss to society and using a proper development strategy to intentionally reduce variation.

Take Free Mock Test on Six Sigma Green Belt

Apply for Certification Exam !!

Certified Six Sigma Green Belt Professional