Probability is a measure of the likeliness that an event will occur. Probability is used to quantify an attitude of mind towards some proposition of whose truth we are not certain.
Concepts
Basic probability concepts and terminology is discussed below
- Probability – It is the chance that something will occur. It is expressed as a decimal fraction or a percentage. It is the ratio of the chances favoring an event to the total number of chances for and against the event. The probability of getting 4 with a rolling of dice, is 1 (count of 4 in a dice) / 6 = .01667. Probability then can be the number of successes divided by the total number of possible occurrences. Pr(A) is the probability of event A. The probability of any event (E) varies between 0 (no probability) and 1 (perfect probability).
- Sample Space – It is the set of possible outcomes of an experiment or the set of conditions. The sample space is often denoted by the capital letter S. Sample space outcomes are denoted using lower-case letters (a, b, c . . .) or the actual values like for a dice, S={1,2,3,4,5,6}
- Event – An event is a subset of a sample space. It is denoted by a capital letter such as A, B, C, etc. Events have outcomes, which are denoted by lower-case letters (a, b, c . . .) or the actual values if given like in rolling of dice, S={1,2,3,4,5,6}, then for event A if rolled dice shows 5 so, A ={5}. The sum of the probabilities of all possible events (multiple E’s) in total sample space (S) is equal to 1.
- Independent Events – Each event is not affected by any other events for example tossing a coin three times and it comes up “Heads” each time, the chance that the next toss will also be a “Head” is still 1/2 as every toss is independent of earlier one.
- Dependent Events – They are the events which are affected by previous events like drawing 2 Cards from a deck will reduce the population for second card and hence, it’s probability as after taking one card from the deck there are less cards available as the probability of getting a King, for the 1st time is 4 out of 52 but for the 2nd time is 3 out of 51.
- Simple Events – An event that cannot be decomposed is a simple event (E). The set of all sample points for an experiment is called the sample space (S).
- Compound Events – Compound events are formed by a composition of two or more events. The two most important probability theorems are the additive and multiplicative laws.
- Union of events – The union of two events is that event consisting of all outcomes contained in either of the two events. The union is denoted by the symbol U placed between the letters indicating the two events like for event A={1,2} and event B={2,3} i.e. outcome of event A can be either 1 or 2 and of event B is 2 or 3 then, AUB = {1,2}
- Intersection of events – The intersection of two events is that event consisting of all outcomes that the two events have in common. The intersection of two events can also be referred to as the joint occurrence of events. The intersection is denoted by the symbol ∩ placed between the letters indicating the two events like for event A={1,2} and event B={2,3} then, A∩B = {2}
- Complement – The complement of an event is the set of outcomes in the sample space that are not in the event itself. The complement is shown by the symbol ` placed after the letter indicating the event like for event A={1,2} and Sample space S={1,2,3,4,5,6} then A`={3,4,5,6}
- Mutually Exclusive – Mutually exclusive events have no outcomes in common like the intersection of an event and its complement contains no outcomes or it is an empty set, Ø for example if A={1,2} and B={3,4} and A ∩ B= Ø.
- Equally Likely Outcomes – When a sample space consists of N possible outcomes, all equally likely to occur, then the probability of each outcome is 1/N like the sample space of all the possible outcomes in rolling a die is S = {1, 2, 3, 4, 5, 6}, all equally likely, each outcome has a probability of 1/6 of occurring but, the probability of getting a 3, 4, or 6 is 3/6 = 0.5.
- Probabilities for Independent Events or multiplication rule – Independent events occurrence does not depend on other events of sample space then the probability of two events A and B occurring both is P(A ∩ B) = P(A) x P(B) and similarly for many events the independence rule is extended as P(A∩B∩C∩. . .) = P(A) x P(B) x P(C) . . . This rule is also called as the multiplication rule. The multiplication rule is used to find out how likely it is for multiple dependent or independent events to happen simultaneously. You use the multiplication rule when finding the probability of both A and B. For example the probability of getting three times 6 in rolling a dice is 1/6 x 1/6 x 1/6 = 0.00463
- Probabilities for Mutually Exclusive Events or Addition Rule – Mutually exclusive events do not occur at the same time or in the same sample space and do not have any outcomes in common. The addition rule finds the probability of occurrence of one or more events. Thus, for two mutually exclusive events, A and B, the event A∩B = Ø, and the probability of events A and B occurring is zero, as P(A∩B) = 0, for events A and B, the probabilities of either or both of the events occurring is P(AUB) = P(A) + P(B) – P(A∩B) also called as addition rule.For example let P(A) = 0.2, P(B) = 0.4, and P(A∩B) = 0.5, then P(AUB) = P(A) + P(B) – P(A∩B) = 0.2 + 0.4 – 0.5 = 0.1
- Conditional probability – It is the result of an event depending on the sample space or another event. The conditional probability of an event (the probability of event A occurring given that event B has already occurred) can be found as
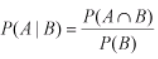
For example in sample set of 100 items received from supplier1 (total supplied= 60 items and reject items = 4) and supplier 2(40 items), event A is the rejected item and B be the event if item from supplier1. Then, probability of reject item from supplier1 is – P(A|B) = P(A∩B)/ P(B), P(A∩B) = 4/100 and P(B) = 60/100 = 1/15.

