Usual Methods of Charging interest
Simple interest: Simple interest in essence is simple as it ignores the effects of compounding. The interest charge is based on the value of the original principal, so interest on interest is not incorporated. This method is typically used to find the interest charge for short-term loans, where ignoring compounding is less of an concern.
Simple interest is determined by multiplying the interest rate by the principal by the number of periods. It is a quick method of calculating the interest on a loan/credit.
Simple Interest = P x I x N
Where P = principal or Loan amount, I = interest rate, N is the duration of loan, using number of periods.
Example 1:
Find simple interest on Rs. 6000 at 7% rate of interest for one year.
Solution:
Let Principal = 6000
Rate of interest = 7%
n=1
Simple interest = P x I x N
= 6000 * 7/100 * 1
= 420
Example 2:
Find simple interest on Rs. 100000 at the rate of 5% for 5 years. Also find the amount for 5 years.
Solution:
Let Principal = 100000 Rs.
Rate = 5%
Time n=5
Amount of simple interest for 5 years is
Interest = P x I x N
=100000 * (5/100) * 5 = 25000
Hence the amount after 5 years = Principal + Interest
=100000 +25000
=125000
Compound Interest: Interest which is calculated not only on the initial principal but also the accumulated interest of prior periods. Compound interest differs from simple interest in that simple interest is calculated solely as a percentage of the principal sum.
The equation for compound interest is: P = C(1+ R/N)NT
Where:
P = future value
C =Capital/ initial deposit
R = interest rate
N = number of times per year interest is compounded
T = number of years invested
Example:
If one invested Rs10,000 at 5% per year, he would earn Rs 2,500 in simple interest after 5 years, i.e Rs 500 for each year. This would give him a total of Rs 12,500 after 5 years.
If he invested Rs 10,000 at 5%, he would earn Rs 2,834 in compound interest after 5 years, giving him a total of Rs 12,834. This is because every month the interest is added to his account and he will earn interest on the interest.
This is how we get to these figures in the example above.
Simple interest on a Rs10,000 investment at 5% per year
| Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
| Deposit | Rs10,000 | Rs0 | Rs0 | Rs0 | Rs0 |
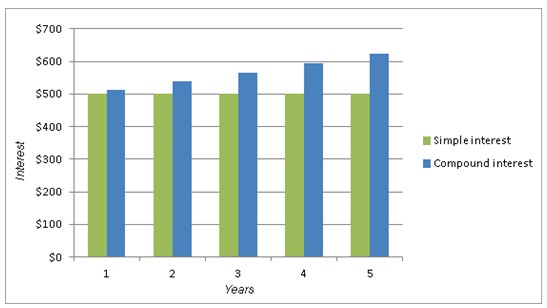
| Interest | Rs500 | Rs500 | Rs500 | Rs500 | Rs500 |
| Total | Rs10,500 | Rs11,000 | Rs11,500 | Rs12,000 | Rs12,500 |
Compound interest on a Rs10,000 investment at 5% per year (compounding monthly)
| Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | |
| Deposit | Rs10,000 | Rs0 | Rs0 | Rs0 | Rs0 |
| Interest | Rs512 | Rs538 | Rs565 | Rs594 | Rs625 |
| Total | Rs10,512 | Rs11,049 | Rs11,615 | Rs12,209 | Rs12,834 |
Comparing compound and simple interest earnings on Rs10,000 at 5% per year
Discounted method
Banks, when discounting bills, apply this method. The Government also issues securities, such as Treasury Bills based on discounting concept.
Example:
Suppose a bank received a request to discount Rs 100000 for 60 days at 5%.
The bank will, after discounting, release Rs. 99,167. In other words a discount of Rs 833 is deducted upfront. Let us see what is the effective rate of interest. It is (833/991670) x (365/60) = 5.11%

