One-Sample Hypothesis Tests

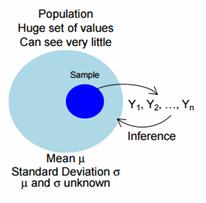
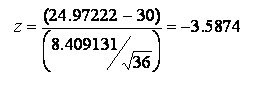A population is identified with the goal of estimating the (unknown) population mean value, identified by µ. You select a random or representative sample from the population where, for notational convenience, the sample measurements are identified as Y1, Y2, …, Yn, where n is the sample size.

Given the data, the best estimate, of µ is the sample mean

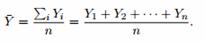
There are two main methods for inferences on µ: confidence intervals (CI) and hypothesis tests. The standard CI and test procedures are based on Y and s, the sample standard deviation.

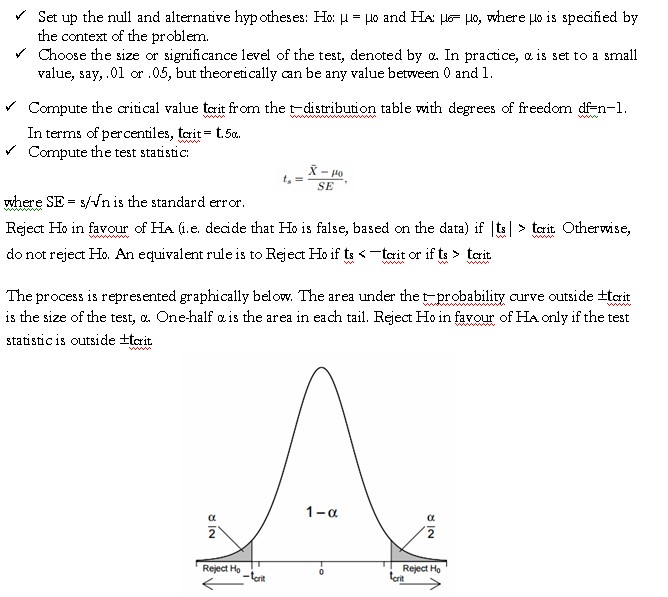
Hypothesis Test for µ Suppose you are interested in checking whether the population mean µ is equal to some pre-specified value, say µ0. This question can be formulated as a two-sided hypothesis test, where you are trying to decide which of two contradictory claims or hypotheses about µ is more reasonable given the observed data. The null hypothesis, or the hypothesis under test, is H0: µ = µ0, whereas the alternative hypothesis is HA: µ6= µ0. At this point, the focus is on the mechanics behind the test. The steps in carrying out the test are

Example

A consumer group, concerned about the mean fat content of a certain grade of burger submits to an independent laboratory a random sample of 12 burgers for analysis. The percentage of fat in each of the burgers is as follows.

21 18 19 16 18 24 22 19 24 14 18 15

The manufacturer claims that the mean fat content of this grade of burger is less than 20%. Assuming percentage fat content to be normally distributed with a standard deviation of 3, carry out an appropriate hypothesis test in order to advise the consumer group as to the validity of the manufacturer’s claim.

For this problem, denoting the percentage fat content by X , then

This value does not lie in the critical region. Thus there is no evidence, at the 5% level of significance, to support the manufacturer’s claim.

Example

In the Speedy Oil Change example, the oil change company claims that it will change customer’s oil in less than 30 minutes on average. However, several complaints have been filed from customers stating that their oil change took longer than 30 minutes and upper-level management at Speedy Oil Change headquarters has requested that you, the manager, investigate the complaints.

Step 1. The first step is to state the hypothesis to be tested, called the null hypothesis, and the alternative hypothesis. The null and alternative hypothesis are denoted Ho and Ha, respectively. If a claim is being tested, as in this example, the claim is stated in the alternative hypothesis. For this example, the null and alternative hypotheses are

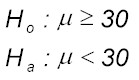
Step 2. Select the level of significance to be used in the test. The level of significance is the probability of rejecting the null hypothesis when it is true. Common significance levels are .10, .05, and .01. Suppose you chose a .05 level of significance, meaning there is a 5% chance that you will reject the null hypothesis when it is true.

Step 3. Select the test statistic that is appropriate for this test.

In general, you will need to decide between using a z test statistic or a t test statistic. A z test statistic is based on the normal distribution and the t test statistic is based on the t-distribution. Your choice comes down to how large your sample size is. Using the t distribution, you locate your critical value based on the degrees of freedom (n-1 for a one-sample test) and the significance level you chose in step 2 (see t table). When n > 30, it is acceptable to use the z value. Why? Remember, as the sample size increases, all sampling distributions converge towards the normal (z). This is the Central Limit Theorem. The generally accepted rule of thumb is that, when n > 30, any sampling distribution can be assumed to be approximately normal. That is why you can use the z values when n > 30. For proof of this, notice that the critical ts, when df=infinity are exactly the same as the critical z’s.

In the Speedy Oil Change example, the sample size is 36, so it is acceptable to use a z test statistic.

The z test statistic for this example is shown below.

Step 4. Determine the rejection region.

The rejection region defines the conditions under which the null hypothesis is rejected. The rejection region depends on the alternative hypothesis stated in Step 1 and the significance level chosen in Step 2. In this example, the rejection region will be found in the lower tail of the standard normal distribution. Why? The rejection region for a one-tailed test can always be located by looking at the direction of the inequality in the alternative hypothesis. Since the alternative hypothesis states μ < 30, the rejection region is in the lower tail of the standard normal distribution. We use the standard normal distribution in this case because we are using the z test statistic which has a standard normal distribution. As stated above, the rejection region also depends on the significance level chosen in Step 2. In this example, a .05 significance level indicates that the rejection region is defined by all the z values that are less than -1.645, which is called the critical value (notice that, if you had chosen to use the t-distribution rather than the z, your critical values would have been -1.69. As you can see, it makes no practical difference whether you use the z or the t when you have large sample sizes. The critical value is the dividing point between the region where the null hypothesis is rejected and the region where it is not rejected. This critical value is found by finding the z value (from a standard normal table) that cuts off the area equal to .05 in the lower tail of the standard normal distribution.

Step 5. Perform the hypothesis test. First, the z test statistic needs to be calculated. The Speedy Oil Change results from the Descriptive Statistics analysis are shown below.