The net present value (NPV) method is the classic economic method of evaluating the investment proposals. It is one of the discounted cash flow (DCF) techniques explicitly recognizing the time value of money. It correctly postulates that cash flow arising at different time periods differs in value and are comparable only when their equivalents. Present values are found out.
The following steps are involved in the calculation of NPV:
- Cash flows of the investment project should be forecasted based on realistic assumptions
- Appropriate discount rate should be identified to discount the forecasted cash flows.
- The appropriate discount rate is the firm’s opportunity cost of capital, which is equal to the required rate of return expected by investors on investments of equivalent risk.
- Present value of cash flows should be calculated using opportunity cost of capital as the discount rate.
- Net present value should be found out by subtracting present value of cash outflows from present value of cash inflows. The project should be accepted if NPV is positive (i.e. NPV> 0).
You will understand better with an example.
Illustration
For example, if the NPV of a project is $1,000, then the value of the firm should increase by $1,000 today. Thus, a project is acceptable if its NPV is positive. If a project has a positive NPV, then it generates a return that is greater than the cost of the funds that are used to purchase the project.
Let the cash flow of an investment (a project) be
{CF 0, CF 1, ••• , CF t}.

Why NPV is Important?
Net present value (NPV) is the true measure of an investment’s profitability. It provides the most acceptable investment rule for the following reasons:
- Time value. It recognizes the time value of money-a $ received today is worth more than a $ received tomorrow.
- Measure of true profitability. It uses all cash flows occurring over the entire life of the project in calculating its worth. Hence, it is a measure of the project’s true profitability. The net present value method relies on estimated cash flows and the discount rate rather than any arbitrary assumptions, or subjective considerations.
- Value additively. The discounting process facilitates measuring cash flows in terms of present values that is in terms of equivalent, current $. Therefore, the net present values of projects can be added. For example, NPV (A+B) =NPV (A) +NPV (B). This is called the value additively principle. It implies that if we know the net present values (NPV) of individual projects, the value of the firm will increases by the sum of their net present values (NPVs). We can also say that if we know values of individual assets, the firm’s value can simply be found by adding their values. The value additively is an important property of an investment criterion because it means that each project can be evaluated, independent of others, on its own merit.
- Shareholder value. The net present value (NPV) method is always consistent with the objective of the shareholder value maximization. This is the greatest virtue of the method.
A question may be raised: why a financial manager should invest Rs 2.500 in Project X? Project X should be undertaken if it is best for the company’s shareholders; they would like their shares to be as valuable as possible. Let us assume that the total market value of a hypothetical company is Rs 10.000. Which includes Rs 2.500 cash that can be invested in Project X.? Thus the value of the company’s other assets must be Rs 7.500. The company has to decide whether it should spend cash and accept Project X or to keep the cash and reject Project X. Clearly Project X is desirable since its PV (Rs 2.725) is greater than the Rs 2.~00 cash. n.: Project X is accepted. The total market value of the firm will be: Rs 7.500 + PV of Project X = Rs 7.500 + Rs 2.725 = Rs 10.225; that is an increase by Rs 225. The company’s total market value would remain only Rs 10.000 if Project X is rejected.
Why should the PV of Project X reflect in the company’s market value? To answer this question, let us assume that a new company X with Project X as the only asset is formed. What is the value of the company? We know from our earlier discussion in Chapter 8 that the market value of a company’s shares is equal to the present value of the expected dividends. Since Project X is the only asset of Company X, the expected dividends would be equal to the forecasted cash flows from Project X. Investors would discount the forecasted dividends at a rate of return expected on securities equivalent in risk to company X. The rate used by investors to discount dividends is exactly the rate which we should use to discount cash flows of Project X. The calculation of the PV of Project X is a replication of the process, which shareholders will be following in valuing the shares of company X. Once we find out the value of Project X, as a separate venture, we can add it to the value of other assets to find out the portfolio value.
The difficult part in the calculation of the PV of an investment project is the precise measurement of the discount rate. Funds of return (10%), in addition to the initial cash outlay (Rs 2,500), to distribute immediately to its shareholders and by the end of the projects’ life to have paid off all the capital raised and return on it 1 The point is illustrated by the calculations shown in Table below. available with a company can either be invested in projects or given to shareholders. Shareholders can invest funds distributed to them in financial assets. Therefore, the discount rate is the opportunity cost of investing in projects rather than in capital markets. Obviously, the opportunity cost concept makes sense when financial assets are of equivalent risk as compared to the project An alternate interpretation of the positive net present value of an investment is that it represents the maximum amount a firm would be ready to pay for purchasing the opportunity of making investment, or the amount at which the firm would be willing to sell the right to invest without being financially worse-off. The net present value (Rs 225) can also be interpreted to represent the amount the firm could raise at the required rate of return (10%), in addition to the initial cash outlay (Rs 2,500), to distribute immediately to its shareholders and by the end of the projects’ life to have paid off all the capital raised and return on it. Details are in table below.
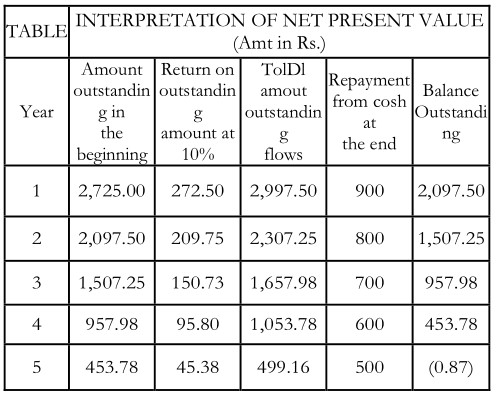
Calculations in Table are based on the assumption that the firm chooses to receive the cash benefit resulting from the investment in the year it is made. Any pattern of cash receipts, such that, the net present value is equal to Rs 225, can be selected. Thus. if the firm raises Rs 2,500 (the initial outlay) instead of Rs 2,725 (initial outlay plus net present value) at 10 per cent rate of return, at the end of fifth year after having paid the principal sum together with interest, it would be left with Rs 363, whose present value at the beginning of the first year at 10 per cent discount rate is Rs 225. It should be noted that the gain to shareholders would be more if the rate of raising money is less than 10 per cent.
Acceptance Rules
It should be clear that the acceptance rule using the NPV method is to accept the investment project if its net present value is positive (NPV> 0) and to reject it if the net present value is negative (NPV < 0). The market value of the firm’s share would increase if projects with positive net present values were accepted. This will be so because the positive net present value will result only if the project would generate cash inflows at a rate higher than the opportunity cost of capital. A project may be accepted if NPV = 0. A zero NPV implies that project generates cash flows at a rate just equal to the opportunity cost of capital. Thus the NPV acceptance rules are:
- Accept NPV > 0
- Reject NPV < 0
- May accept NPV = 0
The NPV method can be used to select between mutually exclusive projects; the one with the higher NPV should be selected. Using the NPV method, projects would be ranked in order of net present values; that is, first rank will be given to the project with highest positive net present value and so on.
Evaluation of the NPV Method
NPV is the true measure of an investment’s profitability. The NPV method, therefore, provides the most acceptable investment rule.
- It recognizes the time value of money-a rupee received today is worth more than a rupee received tomorrow.
- It uses all cash flows occurring over the entire life of the project in calculating its worth. The NPV method relies on estimated cash flows and the discount rate rather than any arbitrary assumptions, or subjective considerations.
- The discounting process facilitates measuring cash flows in terms of present values; that is, in terms of current rupee. Therefore, the NPV s of projects can be added. For example, NPV (A + B) = NPV (A) + NPV (B). This is called the value-additively principle, and it implies that if we know the NPV s of separate projects, the value of the firm will increase by the sum of their NPV s. We can also say that if we know values of separate assets, the firm’s value can simply be found by adding their values. The value-additively is an important property of an investment criterion because it means that each project can be evaluated, independent of others, on its own merit. We will see later on that the value-additively principle is not applicable in the alternative investment criteria.
- The NPV method is always consistent with the objective of maximizing the shareholders’ wealth. This is the greatest virtue of the method.
The NPV method is easy to use if forecasted cash flows and the discount rate are known.
In practice, it is quite difficult to obtain the estimates of cash flows due to uncertainty and to precisely measure the discount rate. Further, caution needs to be applied in using the NPV method when alternative projects with unequal lives, or under funds constraint are evaluated.
It should be noted that the ranking of investment projects as per the NPV rule is not, independent of the discount rates. Let us consider two projects A and B both costing Rs 50 each. Project A returns Rs 100 after one year and Rs 25 after two years. on the others hand, Project B returns Rs 30 after one year and Rs 100 after two years. At discount rates of 5 per cent and 10 per cent, the’ NPV of projects and their ranking are as follows:
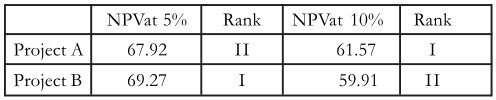
It can be seen that the project ranking is reversed when the discount rate is changed from 5 per cent to 10 per cent the reason lies in the cash flow patterns. The impact of the discounting becomes more severe for the cash flow occurring later in the life of the project; the higher the discount rate, the higher would be the discounting impact. In the case of Project B, the larger cash flows come later in the life. Their present value will decline as the discount rate increases.

