Fan = A (1 + r)n-1+ A (1 + r) n- +…………
………………………………………..……+ A (1 + r)1 + A (1 + r)0
When we take out A in every item, the series is as below:
(1 + r)n-1 + (1 + r) n- +……………
……………………………………..…………+ (1 + r)1 + (1 + r)0
We may rewrite the series as below also:
(1 + r)0 + (1 + r)1 + ………………… .
………………………………………………….+ (1 + r) n-2 + (1 + r)n-1
This series of n terms is in Geometric Progression with a common ratio. The Common Ratio is arrived at by dividing the following term by the preceding term in the series.
Let us take the first term (1 + r)0 which is 1 (anything raised to the power of 0 is equal to 1). Dividing the second term by the first term 1, we get (1 + r) i.e. (1 + r)1 / 1. Next we shall divide the third item (1 + r)2 by (1 + r)1 which is again (1 + r). Hence the Common Ratio in our series is (1 + r).
We get Son by adding the above n number of terms in the series
Son = (1 + r)0 + (1 + r)1 +.….+ (1 + r) n-2 + (1 + r)n-1 …….Eqn.1
Multiplying both sides by ‘(1 + r)’ we have,
(1+r)Son = (1+r) (1 + r)0 + (1+r) (1 + r)1 + …………………
………………………………………. + (1+r) (1 + r) n-2 + (1+r) (1 + r)n-1
(1+r)Son = (1+r) + (1 + r)2 + …. ………………………..
+ (1 + r) n-1 + (1 + r)n ……………………………………….…Eqn. 2
Now Subtracting Equation 2 from Equation 1, we have\
Son – (1 + r)Sn = 1 – (1 + r)n
Sn [1- (1+r)] = 1 – (1 + r)n
Multiplying with A which was removed in the beginning, the formula is
A {[ (1 + r)n – 1] / r}
Mathematical Derivation of formula for Present Value of an
Annuity
PVAn = A [1 / (1 + r)1] + A[ 1 / (1 + r)2] + ……………
………………………………………………….….+ A[1 / (1 + r)n]
We may rewrite the equation as follows:
PVAn = A [ (1 + r)-1] + A[ (1 + r)-2] + ……………
……………………………………………….….+ A[(1 + r)-n]
When we take out A in every item, the series is as below:
(1 + r)-1 + (1 + r)-2 + ……………….+ (1 + r)-n
This series of n terms is in Geometric Progression with a common ratio. The Common Ratio is arrived at by dividing the following term by the preceding term in the series. Dividing the second term by the first term, we get (1 + r)-1. Next we shall divide the third item (1 + r)-3 by (1 + r)-2 which is again (1 + r)-1. Hence the Common Ratio in our series is (1 + r)- 1.
We get Sn by adding the above n number of terms in the series
Sn = (1 + r)-1 + (1 + r)-2 + ………….+ (1 + r)-n ………Eqn.1
Multiplying both sides by ‘(1 + r)-1’ we have,
(1+r)-1Sn = (1 + r)-1(1 + r)-1 + (1 + r)-2 (1 + r)-1 + ……………
………………………………………………..….+ (1 + r)-n(1 + r)-1
Using the concept of am X an = am+n, we get
(1+r)-1Sn = (1 + r)-2 + (1 + r)-3 + ……………….+ (1 + r)-n-1
…………Eqn. 2
Now Subtracting Equation 2 from Equation 1, we have
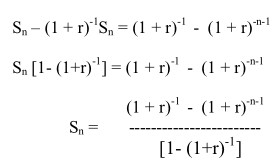
Simplifying the denominator,
1- (1+r)-1 = 1 – 1 = 1+ r – 1 = r
1 + r 1 + r 1 + r
Simplifying the numerator,
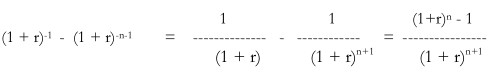
Using the simplified numerator and denominator,
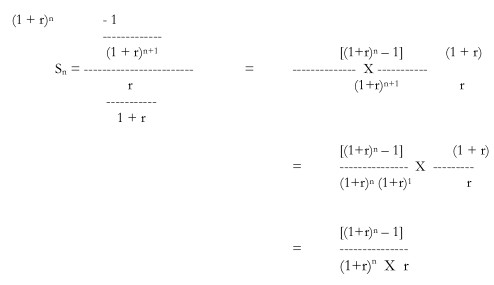
Multiplying with A which was removed in the beginning, the formula is
A {[ (1 + r)n – 1] / [(1+r)n X r]}
Mathematical Derivation of formula for Present Value of an Annuity
PVADn = A {1+[1 / (1 + r)1] + [1 / (1 + r)2] +
……………….+ [1 / (1+r)n-1] }
Multiplying and dividing the whole expression by (1+r), we get
A (1+r) {1+[1 / (1 + r)1] + [1 / (1 + r)2] + ……………….+ [1 / (1+r)n-1] }
——-
(1+r)
A (1+r) {1+[1 / (1 + r)1] + [1 / (1 + r)2] + ……………….+ [1 / (1+r)n-1] } x [1/(1+r)]
A (1+r) {[1 / (1 + r)] + [1 / (1 + r)2] + ……………….+ [1 / (1+r)n] }
Keeping the term A(1+r), the other term is in geometric progression with common ratio as 1/(1+r). Hence applying the formula for sum of geometric progression i.e. Sn = a(rn – 1) / r –1 where a is the first term and r is the common ratio, we get
(1 + r)n – 1 / [(1+r)n X r
Adding the term already removed we have A (1+r) [(1 + r)n – 1
/ [(1+r)n X r]

