The internal rate of return (IRR) method is another discounted cash flow technique, which takes account of the magnitude and timing of cash flows. The internal rate of return (IRR) is the rate that equates the investment outlay with the present value of cash inflow received after one period. This also implied that the rate of return is the discount rate which makes net present value (NPV)=0. Other terms used to describe the IRR method are yield of an investment, marginal efficiency of capital, rate of return over cost, time-adjusted rate of return and so on. IRR is the number that satisfies.
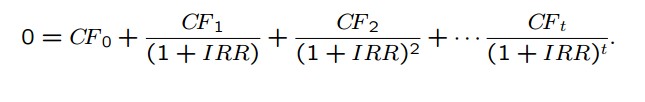
The concept of rate of return is quite simple to understand in the case of a one-period project Assume that you deposit Rs 10,000 with a bank and would get back Rs 10,800 after one year. The true rate of return on your investment would be
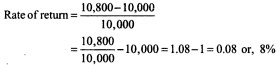
The amount which you would obtain in future (Rs 10,800) would consist of your investment (Rs 10,000) plus return on your investment (.08 x Rs 10,000):
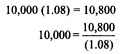
You may observe that i.e., rate of return of your investment (8 per cent) makes the discounted (present) value of your cash inflow (Rs 10,800) equal to your investment (Rs 10,000). We can now develop a formula for the rate of return (r) on an investment (Co) that generates a single cash flow after one period (C 1) as follows:
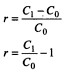
Equation can be rewritten as follows:
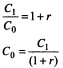
From Equation above, the rate of return can be defined as that rate which equates investment outlay with the present value of inflow received after one period. This also implies that the rate of return is the discount rate which makes NPV = O. This rate may be referred to as the internal rate of return. There is no satisfactory way of defining true rate of return of a long-term asset. The internal rate of return (IRR) is the best available concept. We shall see that although it is a very frequently used concept in finance, yet at times it can be a misleading measure of investment worth.
The internal rate of return can be defined as that rate which equates the present value of cash inflows with the present value of cash outflows of an investment. In other words, it is the rate at which the net present value of the investment is zero. It is called internal rate because it depends solely on the outlay.
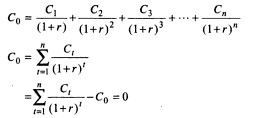
It can be noticed that the IRR equation is the same as the one used for the NPV method with the difference that in the NPV method the required rate of return, k, is assumed to be known and the net present value is found, while in the IRR method the value of r has to be determined at which the net present value is zero.
Uneven Cash Flows: Calculating IRR by Trial and Error
The uneven cash flow method is used to calculate the annual payments needed to fund future college tuition costs. This method uses the cash flow keys on a financial calculator to determine the present value over a period.
The two steps:
- Calculate the present value of the cost of capital over a period.
- Calculate the annual payments that must be made to fund those costs.
The value of r in equation above can be found out by trial and error. The approach is to select any discount rate to compute the present value of cash inflows. If the calculated present value of the expected cash inflow is lower than the present value of cash outflows a lower rate should be tried. On the other hand, a higher value should be tried if the present value of inflows is higher than the present value of outflows. This process will be repeated unless the net present value becomes zero.
Illustration to explains the procedure to calculate the internal rate of return.
A project costs Rs.16,000/- and is expected to generate cash flows of Rs.8,000/- Rs.7,000/- and Rs.6000/- at the end of each year for next 3 years. You know that IRR is the rate at which project will have a zero NPV. As a first step, you try randomly a 20% discount rate. The project’s NPV at 20 % is :
NPV = – Rs.16,000/- + Rs.8,000/-(PVF1, 0.20) + Rs.7,000/-
(PVF2, 0.20) + Rs.6,000/-(PVF3, 0.20)
= – Rs.16,000/- + Rs.8,000/- X 0.833 + Rs.7,000/- X
0.694 + Rs.6,000/- X 0.579
= – Rs.16,000/- + Rs.14,996/- = – Rs. 1,004/-
A negative NPV of Rs.1,004/- at 20 % indicates that the project’s true rate of return is lower than 20 per cent. Now let us try for 16 per cent as the discount rate. At 16 percent, the project’s NPV is
NPV = – Rs.16,000/- + Rs.8,000/-(PVF1, 0.16) + Rs.7,000/-
(PVF2, 0.16) + Rs.6,000/-(PVF3, 0.16)
= – Rs.16,000/- + Rs.8,000/- X 0.862 + Rs.7,000/- X
0.743 + Rs.6,000/- X 0.641
= – Rs.16,000/- + Rs.15,943/- = – Rs. 57/-
Since the project is still negative at 16 percent , a rate lower than 16 percent should be tried. When you select 15 percent as the trial rate, you will find that project’s NPV is Rs.200/-
NPV = – Rs.16,000/- + Rs.8,000/-(PVF1, 0.15) + Rs.7,000/-
(PVF2, 0.15) + Rs.6,000/-(PVF3, 0.15)
= – Rs.16,000/- + Rs.8,000/- X 0.870 + Rs.7,000/- X
0.756 + Rs.6,000/- X 0.658
= – Rs.16,000/- + Rs.16,200/- = Rs. 200/-
The true rate of return should lie between 15 – 16 percent. We can find out a close approximation of the rate of return by the method of linear interpolation as follows: –
Difference
PV required Rs.16,000 200
PV at lower rate, 15% Rs.16,200 257
PV at higher rate, 16% Rs.15,943
R = 15% + (16% – 15%) 200
257
= 15% + 0.8% = 15.8%
Level Cash Flows
There are many situations in which both businesses and individuals would be faced with either receiving or paying a constant amount for a length of period.
When a firm faces a stream of constant payments on a bank loan for a period of time, we call that stream of cash flows an annuity. Individual investors may make constant payments on their home or car loans, or invest a fixed amount year after year to save for their retirement.
Any financial contract that calls for equally spaced and level cash flows over a finite number of periods is called an annuity. If the cash flow payments continue forever, the contract is called perpetuity. Constant cash flows that occur at the end of each period are called ordinary annuities.
An easy procedure can be followed to calculate the IRR for a project that produces level or equal cash flows each period.
Illustration
You assume that an investment would cost Rs. 20,000/-, which provides annual cash inflow of Rs 5,430/- for 6 years. If the opportunity cost of capital is 10 per cent, what is the investment’s NPV? The Rs 5,430 is an annuity for 6 years.
The NPV can be found as follows:
NPV = – Rs 20,000 + Rs 5,430 (PVAF6, 0.10)
= – Rs 20,000 + Rs 5,430 x 4.355 = Rs 3,648
How much is the project’s IRR?
The IRR of the Investment can be found out as follows :
NPV = – Rs 20,000 +Rs 5,430 (PVAFr) = 0
Rs 20,000 = Rs 5,430 (PVAF6,r)
PVAF6,r = Rs.20000= 3.683
Rs.5430
The rate, which gives a PVAF of 3.683 for 6 years, is the project’s internal rate of return.
Looking up PVAF in Table D (Table & formula book) across the 6 years row, you find it approximately under the 16 per cent column. Thus 16 per cent is the project’s IRR, which equates the present value of the initial cash outlay (Rs 20,000) with the constant annual cash inflows (Rs 5,430 per year) for 6 years.
NPV Profile and IRR
IRR rule leads to the same decisions as NPV if
- Cash outflow occurs only at time 0
- Only one project is under consideration
- Opportunity cost of capital is the same for all periods
- Threshold rate is set equal to opportunity cost of capital.
A project is acceptable if its NPV is greater than zero. If a project has an NPV greater than zero, then it generates a return that is greater than the cost of the funds used to purchase the project. A project is acceptable if its IRR is greater than the firm’s required rate of return.
When a project has an IRR greater than the required rate of return, then it generates a return that is greater than the cost of the funds used to purchase the project. Accepting a project using the NPV technique provides the same benefit as accepting a project using the IRR technique.
As a result, both the NPV technique and the IRR technique should always give the same accept/reject decision—that is, if a project is acceptable using the NPV method, it also is acceptable using the IRR method, and vice versa. However, when comparing two or more projects, the two techniques do not always agree as to which project is best. The NPV and IRR methods will return conflicting results when mutually exclusive projects differ in size, or differences exist in the timing of cash flows. When mutually exclusive projects exhibit these attributes, their NPV profiles will cross when plotted on a graph.
Acceptance Rule
The acceptance or rejection rule, using the IRR method is to accept the project if its internal rate of return is higher than the opportunity cost of capital ( r > k). k is also known as the required rate of return, or the cu-off or hurdle rate. The project shall be rejected if its IRR is lower than the opportunity cost of capital (r < k). The decision maker may remain indifferent if the internal rate of return is equal to the opportunity cost of capital. This is the IRR acceptance rule are:
Accept r > k
Reject r < k
May accept r = k
Evaluation of IRR Method
T IRR method recognizes the time value of money and it consider all cash flows occurring the entire life of the project to calculate its rate of return. IRR rule can however; give misleading and inconsistent results when the NPV of a project does not decline with discount rates. It also fails to indicate a correct choice between mutually exclusive projects under certain situations. Unlike in case of NPV method value additively principle does not hold when the IRR method is used – IRRs of project do not add. Thus, for the projects A and B, IRR (A) + IRR (B) need not equal to IRR (A + B).
The following example gives the clarity these characteristics of IRR method: –
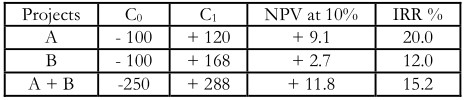
You can see from the example that NPVs of projects add: NPV (A) + NPV(B) = NPV (A + B) = 9.1 + 2.7 = 11.8 IRR(A) + IRR(B) ¹ IRR (A + B) = 20% + 12% ¹ 15.2%
IRR, as an investment decision tool, should not be used to rate mutually exclusive projects, but only to decide whether a single project is worth investing in. IRR overstates the annual equivalent rate of return for a project whose interim cash flows are reinvested at a rate lower than the calculated IRR. IRR does not consider cost of capital; it should not be used to compare projects of different duration. In the case of positive cash flows followed by negative ones and then by positive ones, the IRR may have multiple values.

