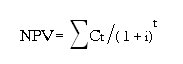Some of the important financial terms used in project finance, are as follows
ROI
Return on Investment (ROI) can be defined as the benefit that an investor yields from an investment of some resource, where a high ROI means the investment’s gains compare favorably to its cost. Primarily ROI is a performance measure, used to assess the efficiency of an investment or compare the efficiencies of several different investments. ROI is a way of relating profits to capital invested.
ROI and the associated metrics gives a snapshot of profitability, adjusted for the size of the investment assets that are blocked in the enterprise.
Return on investment (ROI) = Net income / Investment
Where,
Net income = Gross profit − Expenses
Investment = Stock + Market Outstanding + Claims
or
Return on investment = (Gain from investment – Cost of investment) / cost of investment
or
Return on investment = (Revenue − cost of goods sold) / cost of goods sold (COGS)
Net Present Value (NPV)
Net Present Value (NPV), is the present value (PV) of the total project investments and cash flows required for the proposed project over the entire project period. The basis of NPV lies on the fact that a rupee today is worth more than a rupee tomorrow. Primarily, the NPV is dependent on forecasted cash flows for the project and expected rate of return. NPV is calculated as follows,
Where,
Ct = Refers to the amount of Cash flow (inflow – outflow).
i = discount rate or the rate of return that could be earned on an investment
t = time of the cash flow (year 1, year 2…)
We can determine Net present value (NPV) by calculating the costs (indicating negative cash flow) and benefits (indicating positive cash flows) for each period of an investment. Here, each period is typically one year, but it could also be measured in quarter-years, half-years or months. Once the cash flow for each period is calculated, the present value (PV) of each period is achieved by discounting its future value at a periodic rate of return.
Basically, NPV is the sum of all the discounted future cash flows. NPV is considered as one of the most useful tool to determine whether a project or investment will result in a net profit or a loss. Note, a positive NPV results in profit, while a negative NPV results in a loss. NPV is a measure of excess or shortfall of cash flows, in present value terms, above the cost of funds. Theoretically, a company should pursue every investment with a positive NPV assuming unlimited capital budgeting. However practically, a capital constraints of an organization limits the investments to projects with the highest NPV whose cost cash flows, or initial cash investment, do not exceed the company’s capital. NPV is the most commonly used tool in discounted cash flow (DCF) analysis and is a standardized method for using the time value of money for appraising long-term projects.
NPV can be defined as the difference between the sums of discounted cash inflows and cash outflows. NPV primarily compares the present value of money today to the present value of money in the future, by taking into consideration the inflation and returns. In case all future cash flows are positive, then the only outflow of cash is the purchase price, such that NPV is the PV of future cash flows minus the purchase price (that is its own PV).
Internal Rate of Return (IRR)
Internal Rate of Return (IRR ), can be defined as the discount rate at which Net Present Value equals to zero. IRR aims at calculating the expected rate of return for the investments required for creation and maintenance of the project. So a project is considered acceptable only if IRR is greater than the expected rate of return.
So we can say that the internal rate of return on an investment/project is the annualized effective compounded return rate of return that sets the net present value of all cash flows (both positive and negative) from the investment equal to zero. Equivalently, IRR it is the discount rate at which the NPV of future cash flows equals the initial investment, and it is also the discount rate at which the total present value of costs (indicating negative cash flows) equals the total present value of the benefits (indicating positive cash flows).
IRR assists the managers in ranking the projects by their overall rates of return rather than their net present values, where the investment having the highest IRR is preferred. IRR eases comparison making it attractive, but there are some limitations to its usefulness. For instance, IRR can be applied only for investments that have an initial cash outflow such as purchase of the investment followed by one or more cash inflows.
Usually, the internal rate of return is used to evaluate the attractiveness of a project or investment. In case the IRR of a new project exceeds a company’s required rate of return, only then that project is desirable but if IRR falls below the required rate of return, then the project should be rejected.
Formula for calculating IRR
0 = P0 + P1/(1+IRR) + P2/(1+IRR)2 + P3/(1+IRR)3 + . . . +Pn/(1+IRR)n
Where, P0, P1, . . . Pn equals the cash flows in periods 1, 2, . . . n, respectively;
IRR equals the project’s internal rate of return.
So in order to calculate IRR using the above formula, one would set NPV equal to zero and solve for the discount rate r, which is here the IRR.
Illustration
Lets say a ABC Ltd. needs to decide whether to purchase a piece of factory equipment for Rs. 300,000 or not. The equipment would only last three years, but it is expected to generate Rs. 150,000 of additional annual profit during those years. ABC Ltd. also assumes that it can sell the equipment for scrap afterward for about Rs. 10,000. Use IRR, for ABC Ltd. to determine whether the equipment purchase is a better use of its cash than its other investment options, which should return about 10%.
Solution
IRR equation for the given situation is,
0 = – 300,000 + (150,000)/(1+.2431) + (150,000)/(1+.2431)2 + (150,000)/(1+.2431)3 + 10,000/(1+.2431)4
After, calculating we can say that IRR is 24.31%, which is the rate that makes the present value of the investment’s cash flows equal to zero. From the above results we can interpret that ABC Ltd. should purchase the equipment as it yields 24.31% return for the organization which is much higher than the 10% return available from other investments.