The Theorem of Central Limit
The central limit theorem is the basis of many statistical procedures. Moreover, the theorem states that,
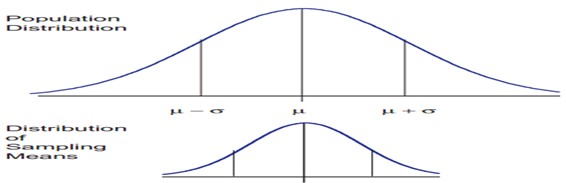
- Firstly, for sufficiently large sample sizes ( n ≥ 30), regardless of the shape of the population distribution. And, if samples of size n are randomly drawn from a population that has a mean µ and a standard deviation σ. Then, there is a normal distribution of samples’ means X.
- Secondly, if there is a normal distribution of populations then, the normal distribution of sample’s means is regardless of the sample sizes.
- Lastly, the theorem states that this distribution of sample means will have the same mean as the original distribution. And, the variability will be smaller than the original distribution tending to be a normal distribution.
Central Limit- Means and Standard deviation
- When there is the use of means as an estimator to make inferences about a population’s parameters and n ≥ 30, the estimator will face normally distribution in constant sampling.
- Moreover, the mean and standard deviation of that sampling distribution is given as µx = µ and σx = σ/√n. However, most points on the chart incline to be near the average with the curve’s shape and the sides tend to be symmetrical.
- And, using ± 3 sigma control limits, the central limit theorem states if there is no change in the process. Then, a sample mean falls outside the control limits an average of only 0.27% of the time.
- Above all, the theorem enables the use of smaller sample averages to evaluate any process. That is to say, distributions of sample means tend to form a normal distribution.
Learn and enhance your knowledge about the Central Limit theorem. Become a Certified TQM Professional Now!

