Bayesian Technique

It makes a great deal of practical sense to use all the information available, old and/or new, objective or subjective, when making decisions under uncertainty. This is especially true when the consequences of the decisions can have a significant impact, financial or otherwise. Most of us make everyday personal decisions this way, using an intuitive process based on our experience and subjective judgments.

Mainstream statistical analysis, however, seeks objectivity by generally restricting the information used in an analysis to that obtained from a current set of clearly relevant data. Prior knowledge is not used except to suggest the choice of a particular population model to “fit” to the data, and this choice is later checked against the data for reasonableness.

Lifetime or repair models, as we saw earlier when we looked at repairable and non repairable reliability population models, have one or more unknown parameters. The classical statistical approach considers these parameters as fixed but unknown constants to be estimated (i.e., “guessed at”) using sample data taken randomly from the population of interest. A confidence interval for an unknown parameter is really a frequency statement about the likelihood that numbers calculated from a sample capture the true parameter. Strictly speaking, one cannot make probability statements about the true parameter since it is fixed, not random.

The Bayesian approach, on the other hand, treats these population model parameters as random, not fixed, quantities. Before looking at the current data, we use old information, or even subjective judgments, to construct a prior distribution model for these parameters. This model expresses our starting assessment about how likely various values of the unknown parameters are. We then make use of the current data (via Baye’s formula) to revise this starting assessment, deriving what is called the posterior distribution model for the population model parameters. Parameter estimates, along with confidence intervals (known as credibility intervals), are calculated directly from the posterior distribution. Credibility intervals are legitimate probability statements about the unknown parameters, since these parameters now are considered random, not fixed.

It is unlikely in most applications that data will ever exist to validate a chosen prior distribution model. Parametric Bayesian prior models are chosen because of their flexibility and mathematical convenience. In particular, conjugate priors (defined below) are a natural and popular choice of Bayesian prior distribution models.

Bayes Formula, Prior and Posterior Distribution Models, and Conjugate Priors

Bayes formula provides the mathematical tool that combines prior knowledge with current data to produce a posterior distribution. Bayes formula is a useful equation from probability theory that expresses the conditional probability of an event A occurring, given that the event B has occurred (written P(A|B)), in terms of unconditional probabilities and the probability the event B has occurred, given that A has occurred. In other words, Bayes formula inverts which of the events is the conditioning event. The formula is

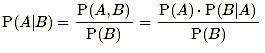
and P(B) in the denominator is further expanded by using the so-called “Law of Total Probability” to write

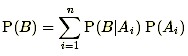
with the events Ai being mutually exclusive and exhausting all possibilities and including the event A as one of the Ai. The same formula, written in terms of probability density function models, takes the form:

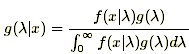
where f(x|λ) is the probability model, or likelihood function, for the observed data x given the unknown parameter (or parameters) λ, g(λ) is the prior distribution model for λ, and g(λ|x) is the posterior distribution model for λ given that the data x have been observed.

When g(λ|x) and g(λ) both belong to the same distribution family, g(λ) and f(x|λ) are called conjugate distributions and g(λ) is the conjugate prior for f(x|λ). For example, the Beta distribution model is a conjugate prior for the proportion of successes p when samples have a binomial distribution. And the Gamma model is a conjugate prior for the failure rate λ when sampling failure times or repair times from an exponentially distributed population. This latter conjugate pair (gamma, exponential) is used extensively in Bayesian system reliability applications.

Bayesian system reliability evaluation assumes the system MTBF is a random quantity “chosen” according to a prior distribution model. Models and assumptions for using Bayes methodology will be described in a later section. Here we compare the classical paradigm versus the Bayesian paradigm when system reliability follows the HPP or exponential model (i.e., the flat portion of the Bathtub Curve).

Classical Paradigm For System Reliability Evaluation

• The MTBF is one fixed unknown value – there is no “probability” associated with it.
• Failure data from a test or observation period allows you to make inferences about the value of the true unknown MTBF.
• No other data are used and no “judgment” – the procedure is objective and based solely on the test data and the assumed HPP model

Bayesian Paradigm For System Reliability Evaluation

• The MTBF is a random quantity with a probability distribution.
• The particular piece of equipment or system you are testing “chooses” an MTBF from this distribution and you observe failure data that follow an HPP model with that MTBF.
• Prior to running the test, you already have some idea of what the MTBF probability distribution looks like based on prior test data or an consensus engineering judgment

Advantages

• Uses prior information – this “makes sense”
• If the prior information is encouraging, less new testing may be needed to confirm a desired MTBF at a given confidence
• Confidence intervals are really intervals for the (random) MTBF – sometimes called “credibility intervals”

Disadvantages

• Prior information may not be accurate – generating misleading conclusions
• Way of inputting prior information (choice of prior) may not be correct
• Customers may not accept validity of prior data or engineering judgements
• There is no one “correct way” of inputting prior information and different approaches can give different results
• Results aren’t objective and don’t stand by themselves