Bases of stratification

The bases of stratification depend on the variable being studied. Since the survey may be interested in May variables, and one, it may be necessary to have stratification on the basis of more than one variable. In view of this, strata should be formed on the basis of major variables. In marketing research, stratification is usually resorted to on the basis of demographic characteristics such as age, sex or income, and geographical distribution of the population such as rural-urban break-up by region, state or city.

Number of Strata: Although theoretically, several strata could be used, on account of practical difficulties, it is desirable to limit the number of strata. Since stratification would enhance the cost of the survey, one has to carefully weigh the benefit resulting from it against the cost involved in its introduction. It is only when the benefits are in excess of the cost that stratification should be introduced. As a rule of thumb, not more than six strata may be used when a single overall estimate is to be made. However, if estimates for certain sub-group of the populations are also required to be made, additional strata may be used.

Sample Sizes within Strata: The third major issue concerning stratification is: How much should the size of each stratum be?

While summing up stratified random sampling, it may be pointed out that it will almost always lead to more reliable estimates than simple random sampling. However, the additional precision achieved would be moderate, while the cost of stratified sampling is generally higher per sampling unit on account of more geographic dispersion of the sample within strata.

Disproportionate Stratified Sampling: The preceding section described stratified sampling which involved the use of the uniform sampling fraction over different strata of the population. At times, it may be preferable to use variable sampling fractions, resulting in disproportionate stratified sampling. When the population in some strata is more heterogeneous than in others, it may be advisable to use variable sampling fractions. The reason is that the use of a uniform sampling fraction may not lead to ‘representative’ samples in such strata. As such, larger sampling fractions may be used in strata with greater variability. Another reason for using disproportionate stratified sampling may be the higher cost per sampling unit in some strata compared to the others. In such a situation, precision can be increased by taking a smaller fraction in the costlier strata and a higher fraction in the cheaper strata. Optimum precision can be obtained for a given cost if the sampling fractions in the different strata happen to be proportional to their standard deviations and inversely proportional to the square root of the costs per unit in the strata. However, in practice, neither the relative variability nor the relative cost of the strata is known. One may find previous surveys dealing with the same or a similar population to be of some guidance in such a situation. Alternatively, one may conduct a pilot survey from which estimates of standard deviations and costs can be obtained. If this too is not possible, one may exercise judgment or use some other measurement in this regard.

A point worth noting is that sampling fractions chosen may be appropriate for one variable or attribute to be studied and may be inappropriate for another. In a survey where one variable or attribute is of considerable importance, it may be advisable to use sampling fractions that are best for it. In all other cases where no priority exists, allocation of sampling fractions to the different strata poses a serious problem. In this context, a major difference between the proportionate and disproportionate stratified samples should be noted. While the former ensures that precision is not reduced as compared to simple random sampling, it is not so in case of the latter. For, an optimum allocation for one variable may result in lower precision than in simple random sampling with respect to another variable. But, gain in precision may not be the only reason for using variable sampling fractions.

Cluster Sampling: Cluster sampling implies that instead of selecting individual units from the population, entire groups or clusters are selected at random. An example will make the concept clear. Suppose we have a population of 25 elements comprising 5 groups, as follows:

Groups	Elements_________
1	X1,	X2,	X3,	X4,	X5
2.	X6,	X7,	X8,	X9,	X10
3.	X11,	X12,	X13,	X14,	X15
4.	X16,	X17,	X18,	X19,	X20
5.	X21,	X22,	X23,	X24,	X25

We are required to choose a probability sample of 10 elements. One way is to select a simple random sample of 10 elements out of the 25. Another way is to select two clusters at random. This may be far more convenient than to use a simple random sample.

For example, if a survey is to be undertaken in a city to collect data from individual households, then, selection of households from all over the city would involve a considerable amount of field work and consequently, would cost more. Instead, a few localities are first chosen. Then, all the households in these localities are covered in the sample. Apart from reduction in cost, such a cluster sample would be desirable in the absence of a suitable sampling frame for the whole population. If, on the other hand, a sample of individual households from the entire city is to be chosen, it will be necessary to first undertake the listing of all households in view of the non-availability of a satisfactory sampling frame. In the case of cluster sampling, such a listing could be confined to only a few localities which are to be entirely covered in the sample.

A few points regarding cluster sampling may be noted here. First, “whether or not a particular aggregate of units should be called a cluster” will depend on the circumstances of each case. In the foregoing example, localities were taken as clusters and households as individual units. In another case, the households may be taken as a cluster and the members of the households as individual units. Second, it is not necessary that cluster should always be natural aggregates such as localities, polling constituencies, schools or classes. Artificial clusters may be formed, as is generally done in area sampling where grids may be determined on the maps. Third, several levels of clusters may be used in any one sample design. Thus, in a city survey, localities or wards, streets and households may be selected in which case localities or wards are the clusters at the first level and streets at the second level.

In our earlier example of 25 elements in 5 clusters, suppose the numerical values are as follows:

1	10	10	10	10	10
2	20	20	20	20	20
3	30	30	30	30	30
4	40	40	40	40	40
5	50	50	50	50	50

The population mean in this case is

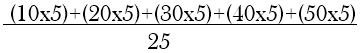
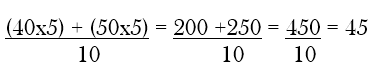
This shows that the mean value from the sample turns out to be only half of the universe mean. This is the minimum sample mean that we can have. In contrast, the maximum sample mean can be obtained if clusters 4 and 5 are chosen. In that case, the sample mean will be

In either case, the sample mean is not realistic. This has happened as the clusters are homogeneous. Suppose the clusters are heterogeneous as follows:

1	10	20	30	40	50
2	10	20	30	40	50
3	10	20	30	40	50
4	10	20	30	40	50
5	10	20	30	40	50

As earlier, a sample of two clusters is selected. Suppose we select the first two clusters, then the sample average will be

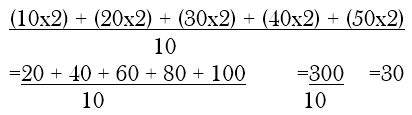
This coincides with the universe mean. It should be obvious, in this case, that whichever two clusters are chosen, the sample average will be 30 because the values of elements in one cluster are the same as in others.

From the foregoing example, we find that a major limitation of cluster sampling is the high degree of intra-cluster homogeneity.

On account of the similarity of one unit in the cluster with its other units, selection of a few clusters may not give a really representative sample. As against this, when clusters have a high degree of intra-cluster heterogeneity, cluster sampling may be more representative.

Multi-Stage Sampling: Multi-stage sampling, as the name implies, involves the selection of units in more than one stage. In such a sampling, the population consists of a number of first stage units, called primary sampling units (PSUs). Each of these PSUs consists of a number of second-stage units. First, a sample is taken of the PSUs, and then a sample is taken of the second-stage units. This process continues until the selection of the final sampling units. It may be noted that at each stage of sampling, a sample can be selected with or without stratification.

An illustration would make the concept of multi-stage sampling clear. Suppose a sample of 5000 urban households from all over the country is to be selected. In such a case, the first stage sample may involve the selection of districts. Suppose 25 districts out of say 500 districts are selected. The second stage may involve the selection of cities, say four from each district. Finally, 50 households from each selected city may be chosen. Thus, one would have a sample of 5000 urban households, arrived at in three stages. It is obvious that the final sampling unit is the household.

In the absence of multi-stage sampling of this type, the process of the selection of 5000 urban households from all over the country would be extremely difficult. Besides, such a sample would be very thinly spread over the entire country and if personal interviews are to be conducted for collecting information, it would be an extremely costly affair. In view of these considerations a sampling from a widely spread population is generally based on multi-stage.

The number of stages in multi-stage sampling varies depending on convenience and the availability of suitable sampling frames at different stages. Often, one or more stages can be further included in order to reduce cost. Thus, in our earlier example, the final stage of sampling comprised 50 households from each of the four selected cities. Since this would involve the selection of households all over the city, it would turn out to be quite expensive and time consuming if personal interviews are to be conducted. In such a case, it may be advisable to select two wards or localities in each of the four selected cities and then to select 25 households from each of the 2 selected wards or localities. Thus, the cost of interviewing as also the time in carrying out the survey could be reduced considerably. It will be seen that an additional stage comprising wards or localities has been introduced here. Thus, this sample has become a four-stage sample-

1st stage – districts

2nd stage – cities

3rd stage – wards or localities

4th and final stage – households

From the preceding discussion, it should be clear that a multi-stage sample results in the concentration of field work. This is turn, leads to saving of time, labour and money. There is another advantage in its use. Where a suitable sampling frame covering the entire population is not available, a multi-stage sample can be used.

Area Sampling: Area sampling is a form of multi-stage sampling in which maps, rather than lists or registers, are used as the sampling frame. This method is more frequently used in those countries which do not have a satisfactory sampling frame such as population lists.

In area sampling, the overall area to be covered in a survey is divided into several smaller area within which a random sample is selected. Thus, for example, a city map can be used for area sampling. Various blocks can be identified on the map and this can provide a suitable frame. The entire city area can be divided into these blocks which are then numbered and from which a random sample is finally drawn.

In sampling the blocks, stratification and sampling with probability proportional to a measure of size are commonly employed. However, stratification in area sampling is based on geographical considerations. Thus, when blocks are identified and numbered on the map, they can be grouped into some meaningful strata representing the different neighborhoods of the town. The point to emphasize is that these blocks must be identifiable without any difficulty.

On the basis of the blocks thus identified, numbered and assigned to strata, a stratified sample of dwellings can be selected. This can be done in either of two ways. First, a sample of dwellings may be drawn from all the dwellings included in a selected block. Second, blocks may be divided into segments of a more or less equal size, and a sample of these segments can be chosen and finally all the dwellings from the selected segments may be taken in the sample. It will thus be seen that the second method introduces another stage of sampling, namely, segments. Although the above discussion relaters to area sampling with respect to a city or town, the same approach is applicable to a large area, say, a state or a country, the only difference being that one or more additional stages of sampling may have to be introduced. Finally, it may be pointed out that area sampling is perhaps the only possibility if a suitable sampling frame is not available.

Multi-Phase Sampling: A multi-phase sample should not be confused with a multi-stage sample. The former involves a design where some information is collected from the entire sample and additional information is collected from only a part of the original sample. Suppose a survey is undertaken to determine the nature and extent of health facilities available in a city and the general opinion of the people. In the first phase, a general questionnaire can be sent out to ascertain who amongst the respondents had at one time or other used the hospital services. Then, in the second stage, a comprehensive questionnaire may be sent to only these respondents to ascertain what they feel about the medical facilities in the hospitals. This is a two-phase or double sampling.

The main point of distinction between a multi-stage and a multi-phase sampling is that in the former each successive stage has a different unit of sample whereas in the latter the unit of sample remains unchanged though additional information is obtained from a sub-sample.

The main advantage of a multi-phase sampling is that it affects economy in time, money and effort. In our earlier example, if a detailed questionnaire is sent out to a large sample comprising individuals, they would not be able to provide the necessary information. Second, more time will be required. Finally, it will be far more expensive to carry out the survey, especially when personal interviews are involved.

Replicated Sampling: Replicated sampling implies a sample design in which “two or more sub-samples are drawn and processed completely independent of each other” It was first introduced by Mahalnobis in 1936, who used the term inter-penetrating sub-samples.

In replicated sampling, several random sub-samples are selected from the population instead of one full sample. All the sub-samples have the same design and each one of them is a self-contained sample of the population. For example, take the case of a random sample of 100 households. This sample may be divided into, say, 10 equal sub-samples to be assigned to 10 interviewers. Thus, each interviewer may be required to collect information from 10 households.

A replicated sample is particularly chosen on account of the convenience it affords in the calculation of standard error. In many complex sample designs, the calculation of standard error becomes too laborious. This difficulty can be considerably reduced by selecting a replicated sample design. However, in modern times when computers are being increasingly used, the case in calculating standard error has made it somewhat less important. Apart from this advantage, there are certain other advantages of replicated sampling. First, if the size of a sample is too large, it may be advisable to split it up into two or more sub-samples. On sub-sample may be used to get the advanced results of the survey. Second, replicated sampling can indicate the non-sampling errors.

In case where bias may arise from a controllable procedure (question sequence, interviewer bias, and editor bias) each sub- sample can be wholly handled in one way-assigned to one interviewer or editor, or using one questionnaire sequence. A fairly simple variance analysis, comparing variance within and among sub-samples, can detect the presence of bias and its importance, again provided that the sub-samples were randomly selected from the total sample.

However, replicated sampling would not be helpful in undertaking a detailed investigation of bias as the numbers in the separate sub-samples tend to be small. Further, such samples do not reveal any systematic errors that may be more or less common to all interviewers and the compensating errors which cancel each other out over an interviewer’s assignment.

Apart from the above limitations, replicated samples have other disadvantages. If personal interviews are to be conducted, replicated samples turn out to be costlier. Likewise, tabulation costs would be higher than in the case of a single large sample. Finally, replicated samples are more complex to administer.

Sequential Sampling: In sequential sampling, a number of samples n1, n2, n3….n4, are randomly drawn from the population. It is not at all necessary that each sample should be of the same size. Generally, the first sample is the largest, the second is smaller than the first, and the third is smaller than the second, and so on.

A sequential sampling is resorted mainly to bring down the cost and hence the smallest possible sample is used. The desired statistics from first sample, n1, are computed and evaluated. If these statistics do not satisfy the criteria laid down, a second sample is drawn. The results of the first and second samples are added and the statistics are recomputed. This process is continued until the specified criteria are satisfied. The criteria are usually a minimum significance level, a minimum cluster size, or a minimum confidence interval.

The main advantage of sequential sampling is that it obviates the need for determining a fixed sample size before the commencement of the survey. Suppose a firm is to decide whether a new product is to be introduced in the market or not. It feels that if it is able to acquire 15 per cent market share in the country, say, within a period of six months. Now, when the firm has undertaken test marketing, it actually achieved far more than 10 per cent, say, 20 per cent, of the market share and that too within three months of test marketing. The firm may be sure to achieve the 15 per cent national market share within one year even though it may not be possible for it to accurately forecast the test market share at the end of four months.

Quota Sampling: Quota sampling is quite frequently used in marketing research. It involves the fixation of certain quotas, which are to be fulfilled by the interviewers.

Suppose in a certain territory we want to conduct a survey of households. Their total number is 2, 00,000. It is required that a sample of 1 per cent, i.e. 2000 households is to be covered. We may fix certain controls which can be either independent or inter-related. These controls are shown in the following tables.

A sample of 2000 households has been chosen, subject to the condition that 1200 of these should be from rural areas and 800 from the urban areas of the territory. Likewise, of the 2000 households, the rich households should number 150, the middle class ones 650 and the remaining 1200 should be

Independent Controls
Rural	1200	Rich	150
Urban	800	Middle class	650
		Poor	1200
Total	2000	Total	2000

Inter-related Controls
	Rural	Urban	Total
Rich	1200	50	150
Middle class	400	250	650
Poor	700	500	1200
Total	1200	800	2000

From the poor class these are independent quota controls. The second table shows the inter-related quota controls. As can be seen, inter-related quota controls allow less freedom of selection of the units than that available in the case of independent controls.

There are certain advantages in both the schemes. Independent controls are much simpler, especially from the viewpoint of interviewers. They are also likely to be cheaper as interviewers may cover their quotas within a small geographical area. In view of this, independent controls may affect the representativeness of the quota sampling. Inter-related quota controls are more representative though such controls may involve more time and effort on the part of interviewers. Also, they may be costlier than independent quota controls.

In view of the non-random element of quota sampling, it has been severely criticised especially by statisticians, who consider it theoretically weak and unsound.

There are points both in favour of and against quota sampling.

These are given below.

Advantages of Quota Sampling

• It is economical as traveling costs can be reduced. An interviewer need not travel all over a town to track down pre-selected respondents. However, if numerous controls are employed in a quota sample, it will become more expensive though it will have less selection bias.
• It is administratively convenient. The labour of selecting a random sample can be avoided by using quota sampling. Also, the problem of non-contacts and call-backs can be dispensed with altogether.
• When the field work is to be down quickly, perhaps in order to minimise memory errors, quota sampling is most appropriate and feasible.
• It is independent of the existence of sampling frames. Wherever a suitable sampling frame is not available, quota sampling is perhaps the only choice available.

Limitations of Quota Sampling

• Since quota sampling is not based on random selection, it is not possible to calculate estimates of standard errors for the sample results.
• It may not be possible to get a ‘representative’ sample within the quota as the selection depends entirely on the mood and convenience of the interviewers.
• Since too much latitude is given to the interviewers, the quality of work suffers if they are not competent.
• It may be extremely difficult to supervise the control and field investigation under quota sampling.

Judgment Sampling: The main characteristic of judgment sampling is that units or elements in the population are purposively selected. It is because of this that judgment samples are also called purposive samples. Since the process of selection is not based on the random method, a judgment sample is considered to be non-probability sampling.

Occasionally it may be desirable to use judgment sampling. Thus, an expert may be asked to select a sample of ‘representative’ business firms. The reliability of such a sample would depend upon the judgment of the expert. The quota sample, discussed earlier, is in a way a judgment sample where the actual selection of units within the earlier fixed quota depends on the interviewer.

It may be noted that when a small sample of a few units is to be selected, a judgment sample may be more, suitable as the errors of judgment are likely to be less than the random errors of a probability sample. However, when a large sample is to be selected, the element of bias in the selection could be quite large in the case of a judgment sample. Further, it may be consider than the random sampling.

Master Samples: A master sample is one from which repeated sub-samples can be taken as and when required from the same area or population. This was first used in the United States when the US Master sample of agriculture was taken. In these samples, the rural area of over 3000 US counties was divided into segments of about four farms each. “After selecting a systematic sample of 1/8 of the segments, the materials were duplicated and made available, with instruction, at low cost.”

The crucial point to note in respect of master samples is that “the actual sample for each new survey is not selected directly from the entire population, but from a frame of segments and dwellings that was selected earlier from the entire population.” The utility of master samples is limited to a relatively short period for there may be changes in the population, which would distort the representative character of the master samples. In view of this, master samples should be relatively permanent, say, dwellings rather than individuals or households which frequently undergo changes on account of births, deaths and migration. The main advantage of master samples is that they can be expeditiously selected on account of their simplicity. Another advantage is that they are economical, because the same master frame is used for drawing samples for several surveys, as a result of which the cost incurred on the preparation of the master frame is spread over these surveys. Further, on account of this economy in each survey, one can initially spend more to create a good master frame. Thus, economy may lead to improved quality in the listing.

Panel Samples: Panel samples are frequently used in marketing research. In panel samples, the same units or elements are measured on subsequent occasions. To give an example: Suppose that one is interested in knowing the change in the consumption pattern of households. A sample of households is drawn. These households are contacted to gather information on the pattern of consumption, subsequently, say after a period of six months, the same households are approached once again and the necessary information on their consumption is obtained. A comparison of the results of the two sets of data would indicate whether there has been any change, and, if so, to what extent. In fact, the information is collected on a more or less continuous basis with the help of panel samples.

Panel samples are extremely convenient and economical and the cost of drawing a second sample is not incurred. But the main limitation of such samples is that it may be difficult to sustain the interest of individuals included in the panel for a long period. Many respondents on the panel may refuse to be interviewed twice or may give poor answers. In either case the quality of the survey will suffer. Another limiting factor in panel samples is that there may be bias on account of the continued participation in the panel. It is felt that the individual is conditioned to some extent by the fact that data on purchases are reported. In such a case the purchase behaviour of panel members may become different from others not covered by the panel. Furthermore, panel samples may turn out to be more expensive while locating the same sample of respondents after a lapse of, say, a year, when some of them might have migrated to other areas. This would involve travel costs in addition to being difficult.

Convenience Sampling: Convenience sampling, as the name implies, is based on the convenience of the researcher who is to select a sample. This type of sampling is also called accidental sampling as the respondents in the sample are included in it merely on account of their being available on the spot where the survey is in progress. Thus, a researcher may stand at a certain prominent point and interview all those or selected people who pass through that place. A survey based on such a sample of respondents may not be useful if the respondents are not representative of the population. It is not possible in convenience sampling to know the “representativeness” of the selected sample. As such, it introduces an unknown degree of bias in the estimate. In view of this major limitation, convenience sampling should be avoided as far as possible. It may however be more suitable in exploratory research, where the focus is on getting new ideas and insights into a given problem.