Markowitz Model and Efficient Frontier

Markowitz Model and Efficient Frontier

Markowitz model, also known as Modern Portfolio Theory (MPT), is a mathematical framework that helps investors in constructing a diversified investment portfolio that maximizes expected returns for a given level of risk. The Markowitz model involves selecting assets that have low or negative correlations with each other, which helps to reduce portfolio risk. This model also considers the expected returns of each asset and the level of risk associated with each investment.

Efficient frontier is a concept used in portfolio management that represents a set of optimal portfolios that offer the highest possible expected return for a given level of risk. The efficient frontier is determined by plotting the expected return and standard deviation of returns for different portfolios on a graph. The portfolios that fall on the efficient frontier are the ones that offer the highest expected return for a given level of risk, or the lowest level of risk for a given expected return. Investors can use the efficient frontier to determine the optimal mix of assets to maximize expected returns for a given level of risk.

Overall, the Markowitz model and efficient frontier are important tools in portfolio management that help investors make informed decisions about how to allocate their investments. These concepts allow investors to construct diversified portfolios that offer the best possible returns for a given level of risk, and to balance their investments to optimize their expected returns.

Modern Portfolio Theory (MPT) refers to the design of optimal portfolios and its implication for asset pricing. It has undergone tremendous development since Markowitz (1952) first laid out the initial mean-variance framework.

A Markowitz portfolio model is one where no added diversification can lower the portfolio’s risk for a given return expectation (alternately, no additional expected return can be gained without increasing the risk of the portfolio). The Markowitz Efficient Frontier is the set of all portfolios of which expected returns reach the maximum given a certain level of risk.

The Markowitz Efficient Frontier

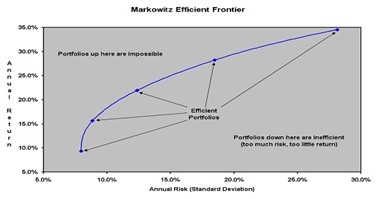
Every possible asset combination can be plotted in risk-return space, and the collection of all such possible portfolios defines a region in this space. The line along the upper edge of this region is known as the efficient frontier. Combinations along this line represent portfolios (explicitly excluding the risk-free alternative) for which there is lowest risk for a given level of return. Conversely, for a given amount of risk, the portfolio lying on the efficient frontier represents the combination offering the best possible return. Mathematically the efficient frontier is the intersection of the set of portfolios with minimum variance and the set of portfolios with maximum return.

The Markowitz model is based on several assumptions concerning the behavior of investors and financial markets.

• A probability distribution of possible returns over some holding period can be estimated by investors.
• Investors have single-period utility functions in which they maximize utility within the framework of diminishing marginal utility of wealth.
• Variability about the possible values of return is used by investors to measure risk.
• Investors care only about the means and variance of the returns of their portfolios over a particular period.
• Expected return and risk as used by investors are measured by the first two moments of the probability distribution of returns-expected value and variance.
• Return is desirable; risk is to be avoided.
• Financial markets are frictionless.

Markowitz model assumes that investors are risk averse. This means that given two assets that offer the same expected return, investors will prefer the less risky one. Thus, an investor will take on increased risk only if compensated by higher expected returns. Conversely, an investor who wants higher returns must accept more risk. The exact trade-off will differ by investor based on individual risk aversion characteristics. The implication is that a rational investor will not invest in a portfolio if a second portfolio exists with a more favorable risk-return profile – i.e., if for that level of risk an alternative portfolio exists which has better expected returns.

Using risk tolerance, one can classify investors into three types: risk-neutral, risk-averse, and risk-lover. Risk-neutral investor’s do not require the risk premium for risk investments; they judge risky prospects solely by their expected rates of return. Risk-averse investors are willing to consider only risk-free or speculative prospects with positive premium; they make investment according the risk-return trade-off. A risk-lover is willing to engage in fair games and gambles; this investor adjusts the expected return upward to take into account the ’fun’ of confronting the prospect’s risk.

 

Back to Tutorial