Reliability Allocation is a method of apportioning a system target reliability amongst sub-systems and components. It is a useful tool at design stage for determining the required reliability of equipment to achieve a given system reliability target.
During the design phase of a product, it is often required to evaluate the reliability of the system. The question of how to meet a reliability goal for the system arises. Reliability Allocation can be used to set reliability goals for individual subsystems so that this goal is met. The simplest method is simply to distribute the reliability goal equally among all subsystems.
However, this rarely gives the best distribution of reliability objectives for all subsystems. It is better to allocate reliability values between the subsystems based on complexity, criticality, achievable reliability, or other factors that are deemed appropriate.
When developing a new product or improving an existing one, engineers are often faced with the task of designing a system that must meet a certain set of reliability specifications. This involves a balancing act in order to determine how to allocate reliability among the subsystems/components in the system.
The apportionment of reliability values between the various subsystems and elements can be made on the basis of complexity, criticality, estimated achievable reliability, or any other factors considered appropriate by the analyst making the allocation. The procedures provided for allocation of software failure rates can be applied to both hardware and system elements provided the user recognizes that these elements typically operate concurrently.
System-level allocations are successively decomposed using the reliability model(s) until an appropriate set of reliability measures has been apportioned to each hardware and hardware/software component of the system.
Reliability allocation involves solving the following inequality:
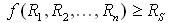
where:
- Ri is the reliability allocated to the ith subsystem/component.
- f is the functional relationship between the subsystem/component and the system.
- Rs is the required system reliability.
Several algorithms for reliability allocation have been developed :
- Equal apportionment
- AGREE apportionment
- ARINC apportionment
- Feasibility of Objectives apportionment
- Repairable Systems apportionment
Equal Apportionment
The simplest apportionment technique is to distribute the reliability uniformly among all components. This method is called Equal apportionment. Equal apportionment assumes a series of n subsystems, all in series and having an exponential failure distribution. Each subsystem is assigned the same reliability. The mathematical model can be expressed as:
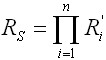
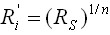
or
where:
- Rs is the system reliability goal.
- R′i is the reliability allocated to the ith subsystem.
- i is the subsystem index.
- n is the total number of subsystems.
AGREE Apportionment
The AGREE apportionment method, designed by the Advisory Group on Reliability of Electronic Equipment, determines a minimum acceptable mean life for each subsystem in order to fulfill a minimum acceptable system mean life. The AGREE method assumes that all subsystems are in series and have an exponential failure distribution. This method takes into account both the complexity and the importance of each subsystem. The mathematical model is:
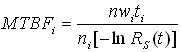
and
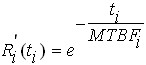
where:
- Rs(t) is the system reliability.
- R′i(ti) is the allocated reliability for the ith subsystem.
- t is the system operating time.
- ti is the operating time of the ith subsystem.
- i is the subsystem index.
- n is the total number of subsystems.
- wi is the importance factor for the ith subsystem.
- ni is the number of sub-elements for the ith subsystem.
- n is the total number of sub-elements, which is given by
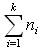
ARINC Apportionment
The ARINC apportionment method was designed by ARINC Research Corporation, a subsidiary of Aeronautical Radio, Inc. The method assumes that all subsystems are in series and have an exponential failure distribution. From the present allocation of the subsystems, allocation improved system failure rates are derived based on weighting factors. The mathematical expression is:
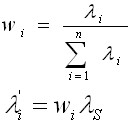
where:
- n is the total number of subsystems.
- λi is the present failure rate of the ith subsystem.
- λS is the required system failure rate.
- λ′i is the failure rate allocated to the ith subsystem.
Feasibility of Objectives
Feasibility of Objectives apportionment is based on numerical ratings of the designs state of the art, the system complexity, the mission operating time and the environment for each item to which the product reliability will be allocated, assuming that all subsystems are in series and have an exponential failure distribution. Ratings are assigned based on the engineer’s experience and judgment. Ratings for each factor range from a low of 1 to a high of 10. These four criteria ratings are multiplied together to get an overall weighting and are normalized so that the product sum is 1. The mathematical model can be described as
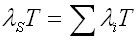
and
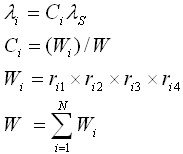
where:
- T is the operating duration.
- λS is the system failure rate.
- λi is the allocated subsystem i failure rate.
- Ci is the percent weighting factors of the ith subsystem.
- Wi is the composite rating for the ith subsystem.
- N is the total number of subsystems.
- rik is the kth rating result for the ith subsystem.
Repairable System Apportionment
Another reliability allocation method, called Repairable Systems apportionment, is designed for repairable systems.
Repairable Systems apportionment allocates subsystem failure rates to allow the system to meet an availability objective for a repairable system. This technique assumes all subsystems to be in series, with exponential failure distributions and constant repair rates. By determining the ratio of the allocated failure rate to the repair rate for each subsystem based on a steady-state availability calculation, the failure rate allocated to each subsystem can be determined. The math expression of this method is:
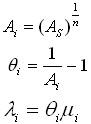
where:
- As is the required system availability.
- Ai is the allocated availability for the ith subsystem.
- n is the total number of subsystems.
- θi is the ratio of allocated failure rate to the repair rate for the ith subsystem.
- ui is the repair rate for the ith subsystem.
- λi is the allocated failure rate for the ith subsystem.

