Evaluating the Credit Decision

The decision model given on page 21 titled ‘The credit decision as a decision problem’ provides a theoretical framework for assessing the risk. One of the methods in evaluating the risk is to determine the payoffs from the alternatives the firm (or individual). The ex-ante payoff of the two situations are:-

Extend credit: PV (Revenue – Costs) x (1 – p) – PV (Cost) x p

Refuse credit: 0

The reward is the revenue earned less the costs. The risk is the partial or complete loss if a default occurs. In evaluating the desirability to taking on credit risk, different situations will have different levels of risk based on

• the probability of default (r) and
• the amount of loss that is expected or actually incurred.

Therefore, lending has a higher exposure (the amount at risk) for the same sized contract than entering into an off-balance sheet derivative agreement such as a swap. If a business undergoes liquidation, the loan might be a write-off, but the risk on the swap relates to the difference between the original value and its replacement cost. It is important to calculate the exposure that will arise if default occurs and this exposure needs to be controlled by setting overall credit limits per individual counterparty.

Businesses make a profit by accepting the risk that the credit may falter. Alternatively nothing is risked if the credit is refused. As most firms have to take risks to earn a return, the decision is slightly more complicated than this simple model. In their daily operations, firms look to trade-off credit risk against the potential gains and losses. The potential losses occur from both accepting bad credits and rejecting good ones.

Modern finance theory implies that declining credit may not necessarily be the proper response to low credit quality. The view of modern theory about risk postulate is that the necessary return should be adjusted for the risk taken. If the risk has been correctly calculated then, losses will be compensated by gains elsewhere.

Finance theory also states that only the systematic risk component needs to be priced. The target of the credit modeling process is to provide estimates of the probable risk. A conclusion can then be made on whether to give a credit line at a risk-adjusted price to compensate for the risk. This is a more complex method than ones used in most organisations which tend to adopt a ‘yes’ or ‘no’ view to extending credit. They also seek to control their exposure via limits on the amounts at risk.

For example, if a business gains a margin of 20% on sales, then it will break-even, that is, it will be indifferent between extending credit and refusing credit if:

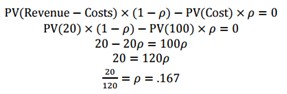
In the above scenario, with a probability of loss of .167, the business is indifferent about accepting a credit risk or declining it. If the lenders are risk averse, then it will need an expected positive payoff to compensate it for risk-taking.

The firm can do two things to increase its sales and still not incur unwanted credit losses. Firstly, it can be indifferent to a higher level of losses if its margin is higher. If the margin is 30%, then it would be indifferent at a loss probability of .23. Conversely, if it can reduce its loss given default, to 80 rather than 100, then the firm can be indifferent with a loss probability of .20.