Future or Compound Value

For finding future value of each cash flow in case of series of cash flows, we can use the formula FVn = PV(1+r)ⁿ or FVn = PV(FVIFrn) and add up to ascertain the Future Value.

Annuities

An annuity is a series of equal cash flows occurring over a specified number of periods. When cash flows occur at the end of each period, it is called an Ordinary Annuity.

Future or Compound Value of Annuity

FVA_n = A (1 + r)^n-1 + A (1 + r) ^n-2+…………………………………. + A (1 + r)1 + A (1 + r)0

FVA_n = A (1 + r)^n-1 + A (1 + r) ^n-2 +………………………………….

…………………………………….…+ A (1 + r)¹ + A (1 + r)0

= A {[ (1 + r)ⁿ – 1] / r}*mathematical derivation is given at the end of the chapter The term [ (1 + r)ⁿ – 1] / r is referred to as the Future Value Interest Factor for an Annuity,

FVAⁿ= A (FVIFA_rn)

Where FVIFA stands for the Future Value Interest Factor of an Annuity at i% for n periods.

Time Line: The series of cash flows can be represented on a time line as below, PV of Re.1 at 5% interest:

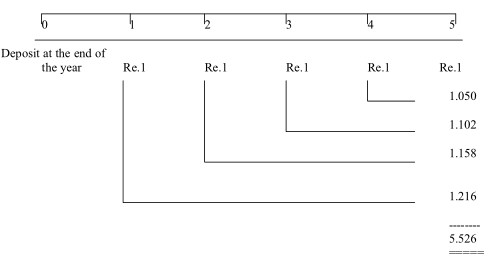
In the above Time Line, the future value for each cash flow is ascertained either by manual calculation of individual item with formula FV = PV (1+r) or by using the Future Value Interest Factor table. Similarly when the cash flows are of equal value at the end of each period as in the Above example i.e. Ordinary Annuity, we can ascertain Future / Compound Value Interest Factor of the Annuity (FVIFA) using the table with the interest rate and the number of years.

FV Annuity Factor

The FV annuity factor formula gives the future total dollar amount of a series of $1 payments, but in problems there will likely be a periodic cash flow amount given (sometimes called the annuity amount and denoted by A). Simply multiply A by the FV annuity factor to find the future value of the annuity. Likewise for PV of an annuity: the formula listed above shows today’s value of a series of $1 payments to be received in the future. To calculate the PV of an annuity, multiply the annuity amount A by the present value annuity factor.

The FV and PV annuity factor formulas work with an ordinary annuity, one that assumes the first cash flow is one period from now, or t = 1 if drawing a timeline. The annuity due is distinguished by a first cash flow starting immediately, or t = 0 on a timeline. Since the annuity due is basically an ordinary annuity plus a lump sum (today’s cash flow), and since it can be fit to the definition of an ordinary annuity starting one year ago, one can use the ordinary annuity formulas as long as a track is kept of the timing of cash flows.

The guiding principle is that before using the formula, the annuity fits the definition of an ordinary annuity with the first cash flow one period away.

Future Value Annuity Factor = (1 + r) N – 1r

Present Value Annuity Factor = (1+ r) N – 1

r (1 + r) N

Where:

r = interest rate

N = number of payments

Example: (FV and PV of ordinary annuity and annuity due)

An individual deposit Rs. 10,000 at the beginning of each of the next 10 years, starting today, into an account paying 9% interest compounded annually. What is the amount of money in the account of the end of 10 years?

Given:

The annuity amount A = Rs. 10,000

The interest rate r = 0.09

Time periods N = 10

Time units are all annual (compounded annually) hence there is no need to convert the units on either r or N. The annuity being described is an annuity due, not an ordinary annuity. In order to use the FV annuity factor, drawing a timeline helps visualize the required actions.

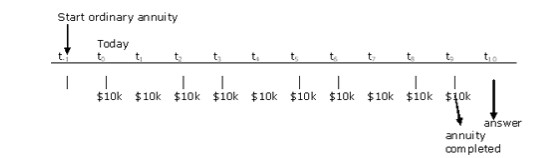
The definition of an ordinary annuity is a cash flow stream beginning in one period, so the annuity being described in the problem is an ordinary annuity starting last year, with 10 cash flows from t0 to t9.

Using the FV annuity factor formula:

FV annuity factor = ((1 + r)N – 1)/r

= (1.09)10 – 1)/0.09

= (1.3673636)/0.09

= 15.19293

Multiplying this amount by the annuity amount of Rs. 10,000, the future value at time period 9 is derived.

FV = (Rs. 10,000) * (15.19293)

= Rs. 151,929

The last step is to calculate value at t10. The future value of a lump sum is used:

FV = PV*(1 + r) N

Where:

N = 1