Learning Resources
 

The List Interface

A List is an ordered Collection (sometimes called a sequence). Lists may contain duplicate elements. In addition to the operations inherited from Collection, the List interface includes operations for the following:

• Positional access — manipulates elements based on their numerical position in the list
• Search — searches for a specified object in the list and returns its numerical position
• Iteration — extends Iterator semantics to take advantage of the list's sequential nature
• Range-view — performs arbitrary range operations on the list.

The List interface follows.

public interface List extends Collection {
    // Positional access
    E get(int index);
    // optional
    E set(int index, E element);
    // optional
    boolean add(E element); 
    // optional
    void add(int index, E element);
    // optional
    E remove(int index);
    // optional
    boolean addAll(int index, Collection c);

    // Search
    int indexOf(Object o);
    int lastIndexOf(Object o);

    // Iteration
    ListIterator listIterator();
    ListIterator listIterator(int index);

    // Range-view
    List subList(int from, int to);
}

The Java platform contains two general-purpose List implementations. ArrayList, which is usually the better-performing implementation, and LinkedList which offers better performance under certain circumstances. Also, Vector has been retrofitted to implement List.

Comparison to Vector

If you've used Vector, you're already familiar with the general basics of List. (Of course, List is an interface, while Vector is a concrete implementation.) List fixes several minor API deficiencies in Vector. Commonly used Vector operations, such as elementAt and setElementAt, have been given much shorter names. When you consider that these two operations are the List analog of square brackets for arrays, it becomes apparent that shorter names are highly desirable. Consider the following assignment statement.

a[i] = a[j].times(a[k]);

The Vector equivalent is:

v.setElementAt(v.elementAt(j).times(v.elementAt(k)), i);

The List equivalent is:

v.set(i, v.get(j).times(v.get(k)));

You may already have noticed that the set method, which replaces the Vector method setElementAt, reverses the order of the arguments so that they match the corresponding array operation. Consider the following assignment statement.

gift[5] = "golden rings";

The Vector equivalent is:

gift.setElementAt("golden rings", 5);

The List equivalent is:

gift.set(5, "golden rings");

For consistency's sake, the method add(int, E), which replaces insertElementAt(Object, int), also reverses the order of the arguments.

The three range operations in Vector (indexOf, lastIndexOf, and setSize) have been replaced by a single range-view operation (subList), which is far more powerful and consistent.

Collection Operations

The operations inherited from Collection all do about what you'd expect them to do, assuming you're already familiar with them. If you're not familiar with them from Collection, now would be a good time to read The Collection Interface section. The remove operation always removes the first occurrence of the specified element from the list. The add and addAll operations always append the new element(s) to the end of the list. Thus, the following idiom concatenates one list to another.

list1.addAll(list2);

Here's a nondestructive form of this idiom, which produces a third List consisting of the second list appended to the first.

List list3 = new ArrayList(list1);
list3.addAll(list2);

Note that the idiom, in its nondestructive form, takes advantage of ArrayList's standard conversion constructor.

Like the Set interface, List strengthens the requirements on the equals and hashCode methods so that two List objects can be compared for logical equality without regard to their implementation classes. Two List objects are equal if they contain the same elements in the same order.

Positional Access and Search Operations

The basic positional access operations (get, set, add and remove) behave just like their longer-named counterparts in Vector (elementAt, setElementAt, insertElementAt, and removeElementAt) with one noteworthy exception: The set and remove operations return the old value that is being overwritten or removed; the Vector counterparts (setElementAt and removeElementAt) return nothing (void). The search operations indexOf and lastIndexOf behave exactly like the identically named operations in Vector.

The addAll operation inserts all the elements of the specified Collection starting at the specified position. The elements are inserted in the order they are returned by the specified Collection's iterator. This call is the positional access analog of Collection's addAll operation.

Here's a little method to swap two indexed values in a List. It should look familiar from Programming 101.

public static  void swap(List a, int i, int j) {
    E tmp = a.get(i);
    a.set(i, a.get(j));
    a.set(j, tmp);
}

Of course, there's one big difference. This is a polymorphic algorithm: It swaps two elements in any List, regardless of its implementation type. Here's another polymorphic algorithm that uses the preceding swap method.

public static void shuffle(List list, Random rnd) {
    for (int i = list.size(); i > 1; i--)
        swap(list, i - 1, rnd.nextInt(i));
}

This algorithm, which is included in the Java platform's Collections class, randomly permutes the specified list using the specified source of randomness. It's a bit subtle: It runs up the list from the bottom, repeatedly swapping a randomly selected element into the current position. Unlike most naive attempts at shuffling, it's fair (all permutations occur with equal likelihood, assuming an unbiased source of randomness) and fast (requiring exactly list.size()-1 swaps). The following program uses this algorithm to print the words in its argument list in random order.

import java.util.*;

public class Shuffle {
    public static void main(String[] args) {
        List list = new ArrayList();
        for (String a : args)
            list.add(a);
        Collections.shuffle(list, new Random());
        System.out.println(list);
    }
}

In fact, this program can be made even shorter and faster. The Arrays class has a static factory method called asList, which allows an array to be viewed as a List. This method does not copy the array. Changes in the List write through to the array and vice versa. The resulting List is not a general-purpose List implementation, because it doesn't implement the (optional) add and remove operations: Arrays are not resizable. Taking advantage of Arrays.asList and calling the library version of shuffle, which uses a default source of randomness, you get the following tiny program  whose behavior is identical to the previous program.

import java.util.*;

public class Shuffle {
    public static void main(String[] args) {
        List list = Arrays.asList(args);
        Collections.shuffle(list);
        System.out.println(list);
    }
}

Iterators

As you'd expect, the Iterator returned by List's iterator operation returns the elements of the list in proper sequence. List also provides a richer iterator, called a ListIterator, which allows you to traverse the list in either direction, modify the list during iteration, and obtain the current position of the iterator. The ListIterator interface follows.

public interface ListIterator extends Iterator {
    boolean hasNext();
    E next();
    boolean hasPrevious();
    E previous();
    int nextIndex();
    int previousIndex();
    void remove(); //optional
    void set(E e); //optional
    void add(E e); //optional
}

The three methods that ListIterator inherits from Iterator (hasNext, next, and remove) do exactly the same thing in both interfaces. The hasPrevious and the previous operations are exact analogues of hasNext and next. The former operations refer to the element before the (implicit) cursor, whereas the latter refer to the element after the cursor. The previous operation moves the cursor backward, whereas next moves it forward.

Here's the standard idiom for iterating backward through a list.

for (ListIterator it = list.listIterator(list.size()); it.hasPrevious(); ) {
    Type t = it.previous();
    ...
}

Note the argument to listIterator in the preceding idiom. The List interface has two forms of the listIterator method. The form with no arguments returns a ListIterator positioned at the beginning of the list; the form with an int argument returns a ListIterator positioned at the specified index. The index refers to the element that would be returned by an initial call to next. An initial call to previous would return the element whose index was index-1. In a list of length n, there are n+1 valid values for index, from 0 to n, inclusive.

Intuitively speaking, the cursor is always between two elements — the one that would be returned by a call to previous and the one that would be returned by a call to next. The n+1 valid index values correspond to the n+1 gaps between elements, from the gap before the first element to the gap after the last one. The following figure shows the five possible cursor positions in a list containing four elements.

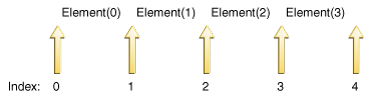
The five possible cursor positions.

Calls to next and previous can be intermixed, but you have to be a bit careful. The first call to previous returns the same element as the last call to next. Similarly, the first call to next after a sequence of calls to previous returns the same element as the last call to previous.

It should come as no surprise that the nextIndex method returns the index of the element that would be returned by a subsequent call to next, and previousIndex returns the index of the element that would be returned by a subsequent call to previous. These calls are typically used either to report the position where something was found or to record the position of the ListIterator so that another ListIterator with identical position can be created.

It should also come as no surprise that the number returned by nextIndex is always one greater than the number returned by previousIndex. This implies the behavior of the two boundary cases: (1) a call to previousIndex when the cursor is before the initial element returns -1 and (2) a call to nextIndex when the cursor is after the final element returns list.size(). To make all this concrete, the following is a possible implementation of List.indexOf.

public int indexOf(E e) {
    for (ListIterator it = listIterator(); it.hasNext(); )
        if (e == null ? it.next() == null : e.equals(it.next()))
            return it.previousIndex();
    // Element not found
    return -1;
}

Note that the indexOf method returns it.previousIndex() even though it is traversing the list in the forward direction. The reason is that it.nextIndex() would return the index of the element we are about to examine, and we want to return the index of the element we just examined.

The Iterator interface provides the remove operation to remove the last element returned by next from the Collection. For ListIterator, this operation removes the last element returned by next or previous. The ListIterator interface provides two additional operations to modify the list — set and add. The set method overwrites the last element returned by next or previous with the specified element. The following polymorphic algorithm uses set to replace all occurrences of one specified value with another.

public static  void replace(List list, E val, E newVal) {
    for (ListIterator it = list.listIterator(); it.hasNext(); )
        if (val == null ? it.next() == null : val.equals(it.next()))
            it.set(newVal);
}

The only bit of trickiness in this example is the equality test between val and it.next. You need to special-case a val value of null to prevent a NullPointerException.

The add method inserts a new element into the list immediately before the current cursor position. This method is illustrated in the following polymorphic algorithm to replace all occurrences of a specified value with the sequence of values contained in the specified list.

public static  
    void replace(List list, E val, List newVals) {
    for (ListIterator it = list.listIterator(); it.hasNext(); ){
        if (val == null ? it.next() == null : val.equals(it.next())) {
            it.remove();
            for (E e : newVals)
                it.add(e);
        }
    }
}

Range-View Operation

The range-view operation, subList(int fromIndex, int toIndex), returns a List view of the portion of this list whose indices range from fromIndex, inclusive, to toIndex, exclusive. This half-open range mirrors the typical for loop.

for (int i = fromIndex; i < toIndex; i++) {
    ...
}

As the term view implies, the returned List is backed up by the List on which subList was called, so changes in the former are reflected in the latter.

This method eliminates the need for explicit range operations (of the sort that commonly exist for arrays). Any operation that expects a List can be used as a range operation by passing a subList view instead of a whole List. For example, the following idiom removes a range of elements from a List.

list.subList(fromIndex, toIndex).clear();

Similar idioms can be constructed to search for an element in a range.

int i = list.subList(fromIndex, toIndex).indexOf(o);
int j = list.subList(fromIndex, toIndex).lastIndexOf(o);

Note that the preceding idioms return the index of the found element in the subList, not the index in the backing List.

Any polymorphic algorithm that operates on a List, such as the replace and shuffle examples, works with the List returned by subList.

Here's a polymorphic algorithm whose implementation uses subList to deal a hand from a deck. That is, it returns a new List (the "hand") containing the specified number of elements taken from the end of the specified List (the "deck"). The elements returned in the hand are removed from the deck.

public static  List dealHand(List deck, int n) {
    int deckSize = deck.size();
    List handView = deck.subList(deckSize - n, deckSize);
    List hand = new ArrayList(handView);
    handView.clear();
    return hand;
}

Note that this algorithm removes the hand from the end of the deck. For many common List implementations, such as ArrayList, the performance of removing elements from the end of the list is substantially better than that of removing elements from the beginning.

The following is a program that uses the dealHand method in combination with Collections.shuffle to generate hands from a normal 52-card deck. The program takes two command-line arguments: (1) the number of hands to deal and (2) the number of cards in each hand.

import java.util.*;

public class Deal {
    public static void main(String[] args) {
        if (args.length < 2) {
            System.out.println("Usage: Deal hands cards");
            return;
        }
        int numHands = Integer.parseInt(args[0]);
        int cardsPerHand = Integer.parseInt(args[1]);
    
        // Make a normal 52-card deck.
        String[] suit = new String[] {
            "spades", "hearts", 
            "diamonds", "clubs" 
        };
        String[] rank = new String[] {
            "ace", "2", "3", "4",
            "5", "6", "7", "8", "9", "10", 
            "jack", "queen", "king" 
        };

        List deck = new ArrayList();
        for (int i = 0; i < suit.length; i++)
            for (int j = 0; j < rank.length; j++)
                deck.add(rank[j] + " of " + suit[i]);
    
        // Shuffle the deck.
        Collections.shuffle(deck);
    
        if (numHands * cardsPerHand > deck.size()) {
            System.out.println("Not enough cards.");
            return;
        }
    
        for (int i = 0; i < numHands; i++)
            System.out.println(dealHand(deck, cardsPerHand));
    }
  
    public static  List dealHand(List deck, int n) {
        int deckSize = deck.size();
        List handView = deck.subList(deckSize - n, deckSize);
        List hand = new ArrayList(handView);
        handView.clear();
        return hand;
    }
}

Running the program produces output like the following.

% java Deal 4 5

[8 of hearts, jack of spades, 3 of spades, 4 of spades,
    king of diamonds]
[4 of diamonds, ace of clubs, 6 of clubs, jack of hearts,
    queen of hearts]
[7 of spades, 5 of spades, 2 of diamonds, queen of diamonds,
    9 of clubs]
[8 of spades, 6 of diamonds, ace of spades, 3 of hearts,
    ace of hearts]

Although the subList operation is extremely powerful, some care must be exercised when using it. The semantics of the List returned by subList become undefined if elements are added to or removed from the backing List in any way other than via the returned List. Thus, it's highly recommended that you use the List returned by subList only as a transient object — to perform one or a sequence of range operations on the backing List. The longer you use the subList instance, the greater the probability that you'll compromise it by modifying the backing List directly or through another subList object. Note that it is legal to modify a sublist of a sublist and to continue using the original sublist (though not concurrently).

List Algorithms

Most polymorphic algorithms in the Collections class apply specifically to List. Having all these algorithms at your disposal makes it very easy to manipulate lists. Here's a summary of these algorithms, which are described in more detail in the Algorithms section.

• sort — sorts a List using a merge sort algorithm, which provides a fast, stable sort. (A stable sort is one that does not reorder equal elements.)
• shuffle — randomly permutes the elements in a List.
• reverse — reverses the order of the elements in a List.
• rotate — rotates all the elements in a List by a specified distance.
• swap — swaps the elements at specified positions in a List.
• replaceAll — replaces all occurrences of one specified value with another.
• fill — overwrites every element in a List with the specified value.
• copy — copies the source List into the destination List.
• binarySearch — searches for an element in an ordered List using the binary search algorithm.
• indexOfSubList — returns the index of the first sublist of one List that is equal to another.
• lastIndexOfSubList — returns the index of the last sublist of one List that is equal to another.