Markov Analysis

1. Introduction
   1. Markov Analysis is a way of analysing the current movement of some variable in an effort to forecast its future movement. As a management tool, Markov analysis has been used during the last several years, mainly as a marketing aid for examining and predicting the behaviour of customers from the standpoint of the loyalty to one brand and their switching patterns to other brands.
   2. In the field of accounting, it can be applied to the behaviour of accounts receivable.

1. Markov Processes
   1. Markov processes (chain or sequence of events) is a stochastic process which is used to analyse decision problems in which the occurrence of a specific event depends on the occurrence of the event immediately prior to the current event. Basically, Markov process helps us to identify
      i.      A specific state of the system being studied, and
      ii.      The state-transition relationship

1. State and Transition Probabilities
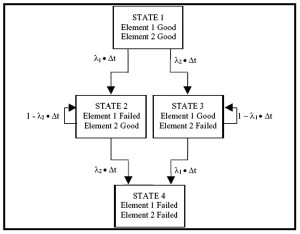
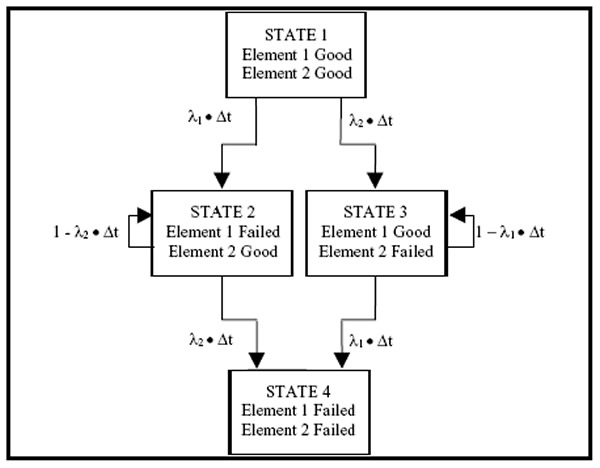
   1. The occurrence of an event at a specified point in time (say, period n) puts the system in a given state, say E_n. If, after the passage of one time unit, another event occurs (during time period n+1), the system has moved from state E_n to state E_n+1.
   2. For example, E_t may represent the number of persons in the queue at a Mother Dairy booth at time t. As time changes to t+1, the state of the queue also changes to E_t+1. The probability of moving from one state to another or remain in the same state in a single time period is called transition probability. Also, since the probability of moving from one state to another depends on the probability of the preceding state, transition probability is called conditional probability.
   3. From the point of view of marketing research, it is assumed that the number of states (brands) are finite and the decision of change of brand is taken periodically, so that such changes will occur over a period of time. In general let,
      i.      E_i = finite number of possible outcomes (i =1, 2, ….., m) of each of the sequence of events (or experiments).
      ii.      p_ij = conditional probability of outcome E_j for any particular event (experiment) given that outcome E_i occurred for the immediately preceding extent (experiment).
   4. The outcomes E₁, E₂, ….., E_m are called states and rhe numbers p_ij are called transition probabilities.

1. Characteristics of a Markov Process
   1. The Markov chain analysis is based on the following assumptions:
      i.      The given system has a finite number of states, none of which “absorbing” in nature (a state is said to be absorbing if a customer would never switch to a particular brand).
      ii.      The states are both collectively exhaustive and mutually exclusive.
      iii.      The probability of moving from one state to another depends only on the immediately preceding state.
      iv.      Transition probabilities are stationary, i.e., they are constant.
      v.      The process has a set of initial probabilities which may be given or determined.
      vi.      The transition probabilities of moving to alternative states in the next time period, given a state in the current time period must sum to unity.

    

Click here for government certification in Quality