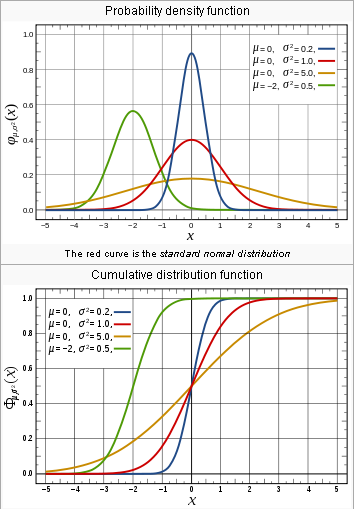
In probability theory, the normal (or Gaussian) distribution is a very commonly occurring continuous probability distribution—that is, a function that tells the probability of a number in some context falling between any two real numbers. For example, the distribution of income measured on a log scale is in some contexts normally distributed, as is often the distribution of grades on a test administered to a large number of people. Normal distributions are extremely important in statistics, and are often used in the natural and social sciences for real-valued random variables whose distributions are not known.
The holding return period formula was introduced previously when discussing time-weighted return measurement. The same formula applies when applied to frequency distributions
(Descriptions changed slightly).
Rt = [(Pt -Pt-1+Dt)/Pt-1]
Where:
Rt = holding period return for time period (t)
Pt = price of asset at end of time period t
Pt – 1 = price of asset at end of time period (t – 1)
Dt = cash distributions received during time t
Apply for Wealth Manager Certification Now!!
http://www.vskills.in/certification/Certified-Wealth-Manager